
GMAT Geometry problems test your spatial reasoning ability. Can you look at a diagram of points, lines, and/or circles and extract the essential details that lead to a correct answer?
If you answered no, well, have no fear! After reading this post, learning the fundamental geometry formulas, and working through these practice geometry questions, you will have the tools you need to succeed on test day!
Table of Contents
- How to Use Geometry Formulas
- GMAT Geometry Practice (Problem Solving Questions)
- Additional GMAT Geoemtry Practice (Data Sufficiency Questions)
How to Use Geometry Formulas
It’s really important to understand that geometry formulas are useful tools, NOT magic wands. Geometry formulas are definitely important! But it could very tempting to think that all you need to do is memorize a bunch of formulas. By themselves, formulas cannot guarantee you a great score on the GMAT Quant section. You also need to know when and how to apply the formulas.
Furthermore, it’s rare that a problem would require only a single formula to solve it. Most often, you’ll need to put a few different formulas together like pieces of a puzzle. The best problem-solvers take a goal-oriented approach. In other words, start with what you need to solve. Then work backward, identifying what info would be useful to get to that goal. In addition, you need to keep in mind the given info, both from the diagram and also from the question statement. Use that to build a bridge to your goal.
This post walks you through the most important formulas for GMAT Geometry. The purpose here is just to help you review—so click on the links to learn more about the material.
Then, you can try out your skills on a set of geometry practice questions. Detailed solutions are given at the very end.
Ready? Let’s go!
Lines and Angles
First of all, know your terms: parallel (same direction) vs. perpendicular (crossing at right angles) lines, interior angles vs. exterior angles, supplementary (angles adding to 180°) vs. complementary (angles adding to 90°).
You should review the basic geometry formulas. For example, this diagram shows all of the possibilities involving a line crossing two perpendicular lines.
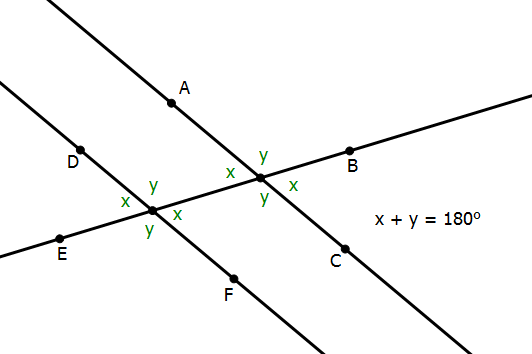
![]() For more review on lines and angles, check out our post on Angles and Parallel Lines on the GMAT and our video lesson Geometry: Lines and Angles.
For more review on lines and angles, check out our post on Angles and Parallel Lines on the GMAT and our video lesson Geometry: Lines and Angles.
Triangles
There are tons of formulas and a huge amount of terminology related to triangles! We can only scratch the surface in this article.
Terminology Related to Sides
- Equilateral – All three sides are equal. All angles are equal to 60°.
- Isosceles – Two equal sides and corresponding equal angles.
- Scalene – None of the sides or angles are equal to one another.
Terminology Related to Angles
- Acute – All three angles measure less than 90°
- Right – One angle is 90° (right)
- Obtuse – One angle is greater than 90°
Sum of angles = 180° (for any triangle)
Pythagorean Theorem: \( a^2 + b^2 = c^2\), where \(a, b\) are the legs and \(c\) is the hypotenuse of a right triangle. (But also try to have memorized the most common Pythagorean Triples: 3-4-5, 5-12-13, 8-15-17, and 7-24-25.)
Area: \(A = \frac{1}{2}bh\), where \(b\) is the base, and \(h\) is the height.
Area of an equilateral triangle with side \(s\): \(A = \frac{3}{2} \cdot \sqrt{3} \cdot s\)
![]()
You can learn more by watching our video lessons, Triangles – Part I and Right Triangles.
And even more resources can be found here:
- Facts about Ordinary Triangles on the GMAT
- The Pythagorean Theorem on the GMAT
- GMAT Math: Area of a Triangle
Quadrilaterals and Other Polygons
The basic area formula for rectangles and parallelograms is: \(A = bh\) (base times height). That’s all you really need for GMAT geometry because more complicated shapes can usually be broken down.
It’s useful to know the following angle formulas:
Sum of interior angles of an \(n\)-sided polygon = \(180(n – 2)\) degrees.
If the polygon is regular (all sides and angles are equal), then any angle has measure \(\frac{180(n – 2)}{n}\) degrees.
![]()
For additional review, check out this video lesson about Regular Polygons.
Circles
Circles show up in many problems on the GMAT test.
Area: \(A = \pi r^2\)
Circumference: \(A = 2\pi r\)
The majority of problems involving circles can be reasoned out without relying on a lot of fancy geometric formulas. You just have to use your mathematical common sense. Need to know the area of a sector? Well just find out what fraction of the whole circle it represents!
Additional resources can be found here:
Solids
There are typically only a couple questions about solid geometry on any given GMAT test. So we won’t delve into that topic here, but you can check out the following links for more.
GMAT Geometry Practice (Problem Solving Questions)
Problem 1
I. 3
II. 4
III. 5
Click here for the answer
E.
All three are possible. (In fact, if you think about it, the number of intersections points could have been any of 0, 1, 2, 3, 4, 5, or 6!)
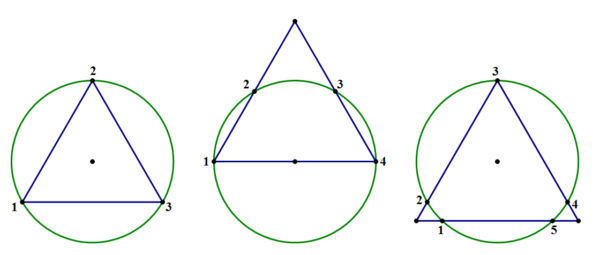
Problem 2
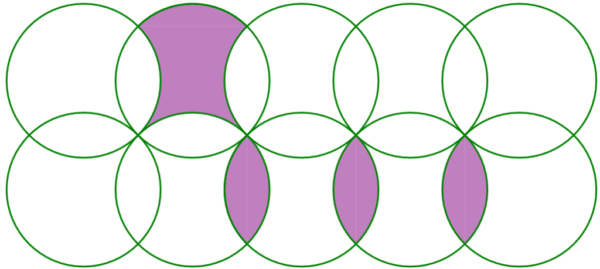
Click here for the answer
B.
It would be a huge mistake to attempt any advanced calculations to solve this. By symmetry, the three smaller shapes can be inserted into the three hollow spaces adjacent to the upper shaded region. Then together, the four shapes will neatly form a single circle. The circle has radius 6, so the area is \(\pi r^2 = \pi 6^2 = 36\pi\).
Problem 3
Click here for the answer
C.
To find the area, we need to know the base and height. Triangle STV is isosceles, so we know that SV = 16 is the base but we don’t know the height.
The height would be represented by a perpendicular line segment from vertex T is bisects base SV, at a point we’ll call W.
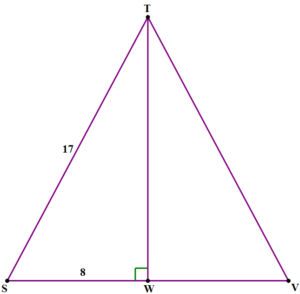
Thus, SW = 8. Now, look at right triangle STW: it has leg = 8 and hypotenuse = 17. It will save you a tremendous amount of calculations here if you already have memorized the 8-15-17 Pythagorean Triple. Thus, TW = 15, and that’s the height. This allows you to find the area: \(\frac{1}{2}\)\(b\)\(h\)\( = \frac{1}{2}\)\((16)\)\((15)\)\( = 120\)
Problem 4
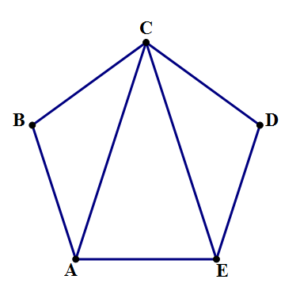
Click here for the answer
Use the formula for the angle of a regular polygon (with \(n=5\)):
\(\frac{180(5 – 2)}{5} = 108\) degrees.
Now, look at isosceles triangle ABC, with an angle of 108° at B. The other two angles are equal: call each \(x\).
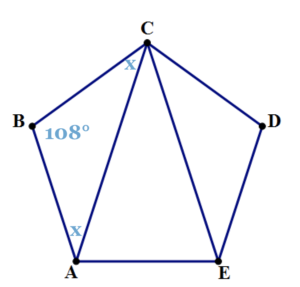
Knowing that the angles in a triangle add up to 180, we know that \(108 + x + x = 180\), which leads to \(x =\) 36°.
Finally, ∠BCA = ∠ECD. Given that ∠BCA = \(x\) = 36°, then ∠ECD = 36°. This means that ∠ACE = 108° − 36° − 36° = 36°
Problem 5
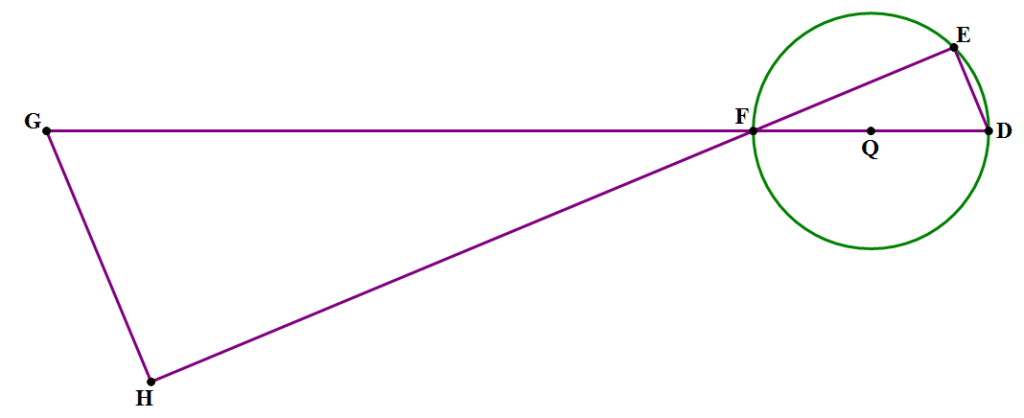
Click here for the answer
B.
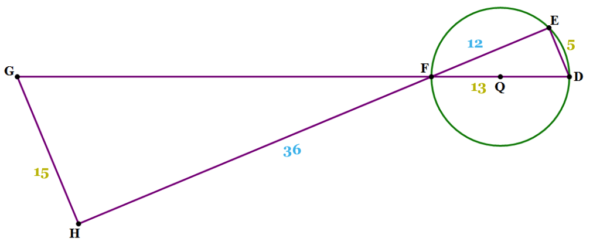
Since ED is parallel to GH, triangles FED and FHG are similar. Why? Well, the vertical angles are equal: ∠GFH = ∠DFE, and the pairs of alternate interior angles are also equal: ∠G = ∠D and ∠H = ∠E.
Let’s begin by focusing on triangle FED. The angle ∠E spans a diameter, so ∠E = 90°. Thus, triangle FED is right with hypotenuse FD = 13 and leg ED = 5. That means that FE = 12 (just remember the 5-12-13 Pythagorean Triple).
Next, since GH = 15 is three times ED, the scaling factor is 3. Scale up FE by 3 to get FH = 36. Finally, find the area using the familiar formula for triangles: \(A = \frac{1}{2}(36)(15) = 270\).
Below is the image again with the length of each side labeled (the givens are in yellow):
Problem 6
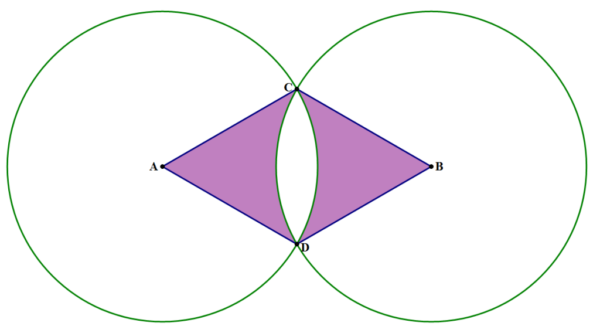
Click here for the answer
D.
This one is definitely tricky! I’ll break up the solution into 5 steps.
Step #1: Each circle has an area of \(\pi(6)^2 = 36\pi\).
Step #2: One sector (“slice of pie”) occupies 60°, which is one sixth of the circle.
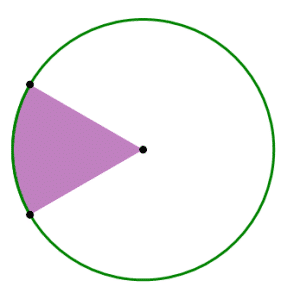
Therefore, the area of the sector is: \(\frac{1}{6}(36\pi) = 6\pi\).
Step #3: Now look at the equilateral triangle.
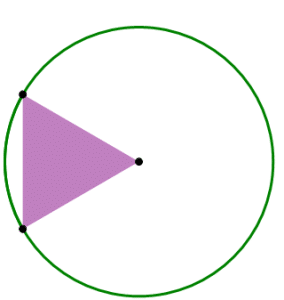
Its side length is \(s = 6\), so using the shortcut formula, its area of the equilateral triangle is \(9\sqrt{3}\).
Step #4: Find the area of the circular segment, which is the name for that little leftover piece, the part of the sector that’s beyond the triangle.
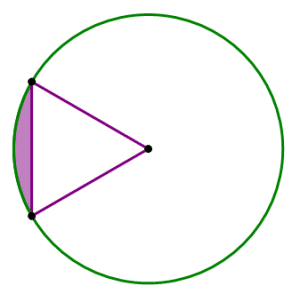
Area of segment = (Area of sector) − (Area of triangle) = \(6\pi – 9\sqrt{3}\).
Step #5: Now notice that the shaded region in the diagram is just the two equilateral triangles minus two circular segments.
\(2(9\sqrt{3}) \) – \( 2(6\pi – 9\sqrt{3})\)\( = 18\sqrt{3} – 12\pi + 18\sqrt{3} = 36\sqrt{3} – 12\pi\)
Problem 7
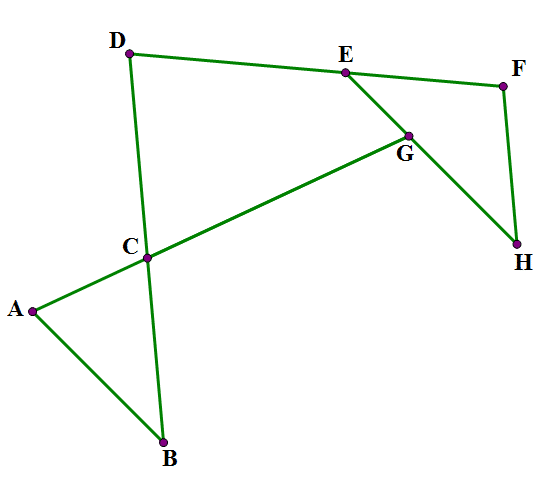
Click here for the answer
D.
Since ∠EGC = 70°, we know that ∠A = 70° (alternate interior angles).
Next, because AB = BC, we see that triangle ABC is isosceles, which means that ∠ACB = 70°. The three angles have to add up to 180°, so this tells us that ∠B = 40°.
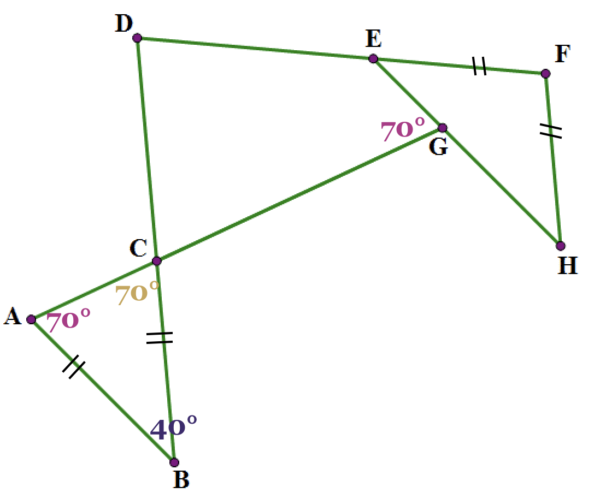
At this point, we reach a very tricky move: both ∠B and ∠H are angles formed by the pairs of parallel lines — the sides of each one are parallel to the corresponding sides of the others. This means ∠B = ∠H = 40°.
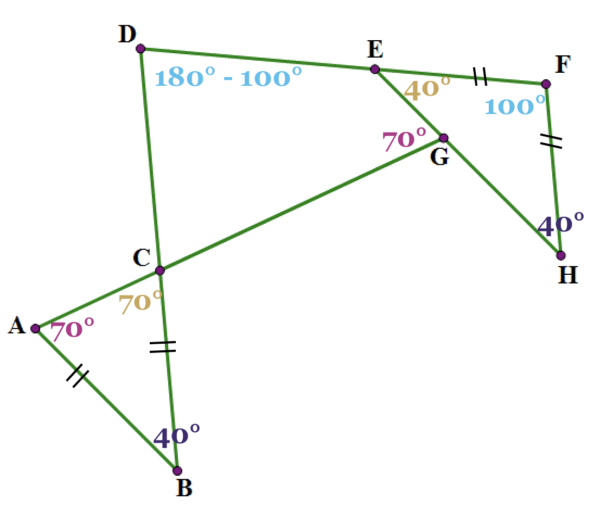
Next, because EF = FH, triangle AFH is also isosceles, which means ∠GEF = 40°. Again, the angles of a triangle have to add up to 180°, so this tells us that ∠F = 100°.
Finally, ∠F and ∠D are two angles on the same side of the same line between two parallel lines (same side interior angles). These angles must be supplementary, which means that ∠D = 180° − 100° = 80°.
Additional GMAT Geoemtry Practice (Data Sufficiency Questions)
The 7 problems above are all of the Problem Solving variety. You can also practice a few Data Sufficiency GMAT geometry questions by following these Magoosh links:
- Geometry Data Sufficiency Problem 1
- Geometry Data Sufficiency Problem 2
- Geometry Data Sufficiency Problem 3 (only available for students with Magoosh’s Premium plan)
- Geometry Data Sufficiency Problem 4
- Geometry Data Sufficiency Problem 5 (only available for students with Magoosh’s Premium plan)
Conclusion
GMAT geometry doesn’t require a huge number of sophisticated formulas. If anything, you should focus more on improving your geometry strategies, particularly how to use diagrams to your benefit.
What is the diagram is telling you: What assumptions can you make? What shouldn’t be assumed? Can you use estimation?
![]() Our video lessons on geometry strategies and estimation will help you build those skills!
Our video lessons on geometry strategies and estimation will help you build those skills!
If you made it to the end of this post, then kudos! Hopefully, you can take what you’ve learned here and apply it to ace the GMAT Quantitative section!



Leave a Reply