First, a few practice problems:
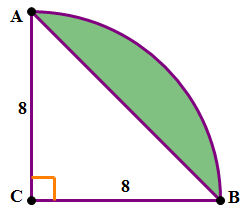
1) In the figure above, AC = BC = 8, angle C = 90°, and the circular arc has its center at point C. Find the area of the shaded region.
2) Employees at a company will vote for an executive team of five people from eight qualified candidates. The executive team consists of a president, a treasurer, and three warrant officers. If an executive team is considered different if any of the same people hold different offices, then how many possible executive teams could be selected from the eight candidates?
-
(A) 56
(B) 120
(C) 210
(D) 1120
(E) 6720
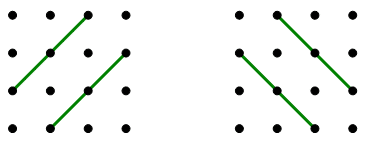
3) In the above diagram, the 16 dots are in rows and columns, and are equally spaced in both the horizontal & vertical direction. How many triangles, of absolutely any shape, can be created from three dots in this diagram? Different orientations (reflections, rotations, etc.) and/or positions count as different triangles. (Notice that three points all on the same line cannot form a triangle; in other words, a triangle must have some area.)
-
(A) 516
(B) 528
(C) 1632
(D) 3316
(E) 3344
What all three of these problems have in common is: relying on formula alone will not help you. Complete explanations will come at the end of this article.
Formulas are useful
Clearly, it’s a good idea to know some GMAT math formulas —– many of the best formulas to know are listed on that blog. Formulas can be wonderful shortcuts, very efficient time-savers. Clearly it would be a mistake to walk into the GMAT Math section without knowing a single formula.
But BEWARE!
Formulas are useful to a point, but one of the worst mistakes folks make when they study for GMAT Math is to think that all they have to do to master the GMAT Math section is to memorize all the formulas. Similarly, the worst way to approach a GMAT math section is to approach each question asking only, “What’s the best formula to use for this question?” That’s roughly the same as thinking that all I need to be the world’s best lion tamer is a fancy hat that says “lion tamer”! In fact, the GMAT regularly designs math questions that predictably punish folks who blindly memorize formulas. Most of the harder math problems on the GMAT have this property: if you approach the problem with the perspective of “what’s the best formula to use to solve this question?”, then you very likely will miss what the question is really about and get it wrong. Here are some tips you can use to escape these traps.
Remember, but don’t memorize
What do I mean by this? Yes, you have to remember some formulas for the GMAT. One option would be to memorize each one separately as an isolate mathematical factoid. Some people are exceptionally good memorizers, but for most people, this is not too helpful: in particular, if, in the stress of the real GMAT, you forget what you memorized, then you are out of luck. Memorizing allows you no recourse if you forget, and it gives you no insight into mathematical logic.
Instead, I would recommend: understand the derivation of every formula: that is, understand the logical argument that underlies the formula and from which the formula arises. Think in terms of “why is it true?”: don’t stop at simply “what is true?” For example, both the permutation and combination formulas can be derived directly from the Fundamental Counting Principle. In another blog, I talked about the derivation of the formula for the area of an equilateral triangle. For most of the formulas you need to know for the GMAT, there is a context of logical argument that is also helpful to know. One exception is Archimedes‘ formula for the area of a circle:
Yes, the great master Archimedes had a brilliant argument for why that formula is true, but that’s well beyond the kind of logic you need to employ on the GMAT. For this one, you can take a pass and simply memorize the formula, if you haven’t already. For most formulas, though, you should explore the logical of the context in depth.
Mathematical thinking
Problem-solving in mathematics is a subtle and sophisticated subject, and even in the limited context of the GMAT math section, the harder questions sometimes demand insightful approaches. Formulas are very cookie-cutter: if you have a formula to do something, it’s very good at doing that one thing, but that one thing is all it can do. That’s quite different from the flexible analyses characteristic of mathematical thinking.
Think about it this way. When you approach the GMAT math section, you should have a well-equipped tool box. The individual formulas you know are tools, but each one is a highly specific tool, useful for only one thing. Other more widely applicable tools are skills such as estimation or backsolving or picking numbers. It’s important to have in your “tool box” a mix of tools, some more general and some more specific; what’s more important, though, it knowing when and how to use them.
Perspective
In the post How to do GMAT Math Faster, I talk in depth about left-brain vs. right-brain thinkers. Left-brain dominant thinkers want to know “what to do,” and they love formulas, because it’s always very clear what to do with a formula. A more right-brain perspective focuses on “how to look at the problem“, on the question of the best way to frame a problem, the best problem-solving perspective to adopt. Often, on a challenging GMAT problem, when one adopts the best perspective, what to do becomes obvious. Given the correct perspective, many test-takers could solve the problem, but most folks get that problem wrong because it’s hard to come up with that right perspective on one’s own. Coming up with the best perspective for a problem, the best way to frame a problem, takes time. It’s a right-brain pattern-matching skill: these always take time & experience to master. It’s very important to read solutions carefully: left-brain thinkers will want to jump ahead to the formulas, to “what to do“, and may be frustrated because they knew all those parts already. To get the most from solutions, it’s very important to study the very beginning, any reasons given for making one perceptual choice rather than another. Sometimes, it may be helpful to solve the problem in more than one way, to experience the difference in different solution routes. Sometimes, the perceptual choices are hard to get from the solution, and the only way to find an answer is to post a question to an expert in the forums, asking them: “why do we get the solution this way but not in that way?” Through asking questions and investigating, over time one develops more of a sense for problem-solving perspective.
Summary
Yes, know the GMAT formulas, but don’t think they are a magic bullet. You will get considerably more from understanding the logic behind each formula, than you will from blind memorization of only the formula. Finally, it’s most important to develop the problem-solving perspective, which will help you to see which formulas to use when. Here’s another practice question from inside the Magoosh product:
4) http://gmat.magoosh.com/questions/124
If you would like to share your own experience with formulas, or would like to clarify something I have said, let us know in the comments section.
Practice problem solutions
1) There’s not a single formula we can use to get the answer, but by combining a few formulas, we can calculate this.
First, think about the circle. The circle has radius r = 8, so its total area would be
This entire figure is a quarter of the circle, so that area would be
Now, the shaded area (technically known as a circular segment), would have an area of
(circular segment) = (quarter circle) – (triangle ABC)
Well, we already have the area of the quarter circle. The triangle would have an area of (1/2)bh = 32. Therefore, the area of the segment is
Answer = (B)
2) We can use a quick formula for this. We have to go back to the Fundamental Counting Principle and think this through.
Choice #1: for the president, we have eight choices
Choice #2: for the treasurer, we have seven remaining choices
Choice #3: we have to pick 3 warrant officers from the remaining 6. This would be
The FCP tells us to multiply the number of choices in each selection:
8*7*20 = 56*20 = 1120 choices — Answer = (D)
3) This is a very subtle counting problem. This post on difficult counting problems may provide some insights.
The basic strategy will be to calculate the total number of sets of three points we can select in this diagram, and then subtract the small number of sets of three collinear points.
The first step: in how many ways can we select three points from a set of 16 points?
There are 560 sets of three points we can select. Right away, notice, we can eliminate answer choices (C), (D), and (E) as too big.
How many sets of three points are collinear? Well, first look at the column. In any column, we have four collinear points, so we could eliminate any one point, and we would be left with a unique set of three collinear points. That means we have four collinear sets in each column, or 16 vertical sets of collinear points. By symmetry, we must have 16 horizontal sets of collinear point. That’s 32 together.
But that’s not all. Notice there are two long diagonals, of four points each: much in the same way as in the argument above, there must be four unique sets of three collinear points along each diagonal. For the two diagonals, that’s 8 more. We up to 40 now.
Now, notice the short diagonals of only three points:
That’s the last four. There are a total of 44 unique sets of three collinear points. Since any of these would not constitute valid triangles, we have to subtract this from the total number of sets of three points.
560 – 44 = 516 —- answer = (A)





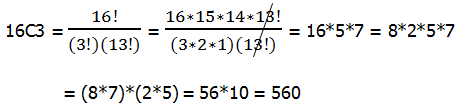




Leave a Reply