The GMAT will ask you about geometric solids. The OG tells you that you should expect questions about rectangular solids and cylinders.
Here, I will discuss four less common solids that are much less likely to appear on the GMAT Math section: the prism, the pyramid, the cone, and the sphere. For all of these, you are unlikely to have to know the technical formulas, and far more likely to be asked questions just testing your general three-dimensional thinking.
Technical Definitions and Formulas (if you want to know them)
The prism
Imagine any polygon. Now, imagine an identical, congruent polygon, placed above it. Now, connect the two congruent polygons with rectangles. That’s a prism.
There are triangular prisms (by far, the most common), as well as rectangular prism (ordinary rectangular solids), pentagonal prisms, hexagonal prisms, etc. I would say your chances of seeing even a triangular prism on the GMAT math is slight.
volume of prism=(area of base)\(*h\)
surface area\(=2*\)(area of base)\(+h*\)(perimeter of base)
The pyramid
Imagine any polygon as a base, and off of each edge, triangles converging at a single point. That’s a pyramid. If you see a pyramid at all on the GMAT, it will in all likelihood be a triangular-base or square base pyramid.
As it happens, \(the volume of a pyramid=(1/3)*(area of base)*h\). Let’s not even discuss the surface area of a general pyramid: it’s a nightmare you definitely do not need to know.
Now, we enter the realm of Archimedes (287 – 212 bce), without a doubt the greatest mathematician in antiquity. Archimedes is the one who figured out that the area of a circle is \(A = \pi*r^2\); the human race knows that fact because of Archimedes. He also figured out everything about the cylinder, the cone, and the sphere.
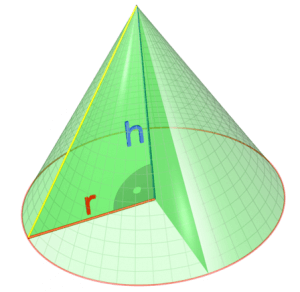
The cone
Basically, the cone is a pyramid with a circle at the bottom instead of a polygon.
The volume of a cone is just like the formula for the volume of a pyramid. Volume of a cone = \(\frac{1}{3}*(area of base)*h = \pi*r^2*\frac{h}{3}\). You are very unlikely to need even a clue about that on the GMAT. As for the surface area of a cone, just forget it.
The sphere
Archimedes was particularly proud of everything he figured out about the sphere. He figured out:
You are extremely unlikely to need to have memorized either of those equations, as beautiful as they may be.
What the GMAT Could Ask About These
First of all, you probably could sit through five GMATs in a row and not see a single question about any of these — though I don’t think sitting through 5 GMAT in a row would be a fabulous way to spend a Saturday. Any question about these would be rare, and would be much more likely to probe your general three-dimensional reasoning skills rather than the specific formulas associated with these shapes. Here are a few examples:
Practice Problems
1) A sphere is surrounded by the smallest cylinder that will just contain it. Which of following is a complete set of the points where the cylinder touches the sphere?
I. One point
II. Two points
III. A Circle
(A) I only
(B) II only
(C) III only
(D) I & III
(E) II & III
(BTW, this diagram: sphere inscribed in a cylinder, is the diagram that was carved on Archimedes’ tombstone, at his request.)
2) A pyramid has a square base of 6 cm, and the four lateral faces are four congruent equilateral triangles. What is the total surface area of the pyramid in square cm?
(A) \(36 + 18*\sqrt{3}\)
(B) \(36 + 36*\sqrt{3}\)
(C) \(72\)
(D) \(72 + 36*\sqrt{3}\)
(E) \(72 + 72*\sqrt{3}\)
3) A rectangular solid, 3 x 4 x 12, is inscribed in a sphere, so that all eight of its vertices are on the sphere. What is the diameter of the sphere?
(A) 13
(B) 15
(C) 18
(D) 19
(E) 20
4) The octahedron is an eight-faced geometric solid that can be thought of as two square-based pyramids with the squares glued together. All eight faces of the octahedron are congruent equilateral triangles. Given that an edge is where the side of one equilateral triangles is attached to the side of another equilateral triangle, how many edges does the octahedron have?
(A) 8
(B) 10
(C) 12
(D) 16
(E) 18
5) Suppose you have three identical prisms with congruent equilateral triangles as the end-polygons. Suppose you attach them by the rectangular faces so they are perfectly aligned. There will be some large faces created by two or more co-planar faces of the individual prisms: count each such large face as one. Given that, how many faces does the resultant solid have?
(A) 4
(B) 6
(C) 9
(D) 10
(E) 12
Practice Problem Answers
(1) E; (2) B; (3) A; (4) C; (5) B
Practice Problem Explanations
(1) Let’s use the familiar reference points of Earth’s geography to talk about the sphere. The cylinder fits the sphere tightly, so it touches the sphere around its “equator.” The top of the cylinder touches the “north pole” of the sphere, and the bottom of the cylinder symmetrically touches the “south pole” of the sphere. That’s a circle (the equator) and two points (the north & south poles). Answer E.
(2) First of all, of course, the base has an area of 36. For the lateral surfaces, it would be helpful to remember the formula for the area of an equilateral triangle. If that’s unfamiliar, take a look at this post: https://magoosh.com/gmat/gmat-math-memory-vs-memorizing/
The area of one equilateral triangle is \(A = \frac{s^2*\sqrt{3}}{4}\). We know the side of the equilateral triangle must be the same as the square: \(s = 6\). Thus, one of these equilateral triangles has an area of \(A = \frac{6^2*\sqrt{3}}{4} = 9*\sqrt{3}\). There are four identical triangles, so their combined area is \(A = 36*\sqrt{3}\). Now, add the square base, for a total surface area of \(A = 36 + 36*\sqrt{3}\). Answer = B
(3) First of all, what’s important to appreciate — and this is something that does appear with some frequency on the GMAT math section — the most famous formula in mathematics, the Pythagorean theorem, extends seamlessly to three-dimensions. If you have a solid with a length L, a width W, and a height H, then the “space diagonal”, the line form one vertex to the catty-corner opposite vertex, has a length R, which satisfies the equation: \(Y^2 = L^2 + W^2 +H^2\).
Here, we can easily find the space diagonal of the 3 x 4 x 12 solid. We get
\(Y^2 = 3^2 + 4^2 + 12^2\)
\(Y^2 = 9 + 16 + 144 = 169\)
\(Y = \sqrt{169} = 13\)
So the space diagonal of the rectangular solid is 13. It may stretch your visualizing abilities a bit, but this space diagonal must be equal to the diameter of the sphere — the line from one vertex to the catty-corner opposite vertex must pass through the center of the sphere, and a line segment from one point on a sphere to another that passes through the center is, by definition, a diameter.
So diameter = space diagonal = Y = 13. Answer = A
(4) Again, we will use the analogy of Earth’s geography to orient us. (This, in and of itself, is a useful trick to remember.) When we glue together the two square faces, call that the “square equator” of the octagon. That’s a square, so obviously it have four edges. The pyramid above that goes up to a “north pole vertex”, and four edges run down that vertex to the corners of the “square equator,” so that’s four more. Similarly and symmetrically, the upside-down pyramid underneath comes to a point at the “south pole vertex”, with an additional four edges running from that vertex to the “square equator.” That’s four edges on the “square equator”, four more above, four more below, for a total of twelve edges on the octahedron. Answer = C
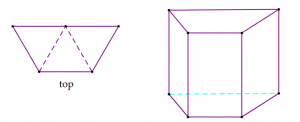
(5) The resultant figure looks something like this:
The top and the bottom are each single faces formed by three equilateral triangles joining, as in the diagram on the left, to make an isosceles trapezoid. Top = 1 face, and bottom = 1 face. This is a four-sided figure, so there are four rectangles extending from the bottom of this prism to the congruent figure at the top. Notice, in particular, the larger vertical face in the “back” of the diagram to the right is formed by two faces of the original triangular prisms lying next to each other and smoothly joining. Total = 1 top + 1 bottom + 4 sides = 6 faces. Answer = B.







Leave a Reply