If you haven’t been following our series on RTD tables, take a few minutes to catch up:
- Using Diagrams to Solve Rate Problems: Part 1
- Using Diagrams to Solve Rate Problems: Part 2
- A Different Use of the RTD Table: Part 1
- A Different Use of the RTD Table: Part 2
- Using the RTD Table for a Complicated Problem
- One More RTD Table Problem: Average Rates Part 1
Yesterday we solved this problem:
Div’s bicycle tour consists of three legs of equal length. For the first leg Div averaged 16 kilometers per hour. For the second leg he averaged 24 kilometers per hour. What speed must Div average for the final leg in order to average 24 kilometers per hour for the entire tour?
A) 20 kilometers per hour
B) 28 kilometers per hour
C) 32 kilometers per hour
D) 40 kilometers per hour
E) 48 kilometers per hour
We made a pretty good use of the RTD table, but we still took quite a while to arrive at our answer, and we did a lot of computation and algebra, every step inviting some sort of error.
There are two shortcuts that could save us some time and energy while reducing opportunities for computational error.
The big shortcut.
Notice that this problem doesn’t specify the lengths of the legs, but that every answer is a constant. That implies that so long as the legs are all of the same length as required by the problem, any leg length will yield the same answer.
Let’s take advantage of that fact to avoid some unnecessary algebra. Let’s stipulate an easy leg length. What leg length would be easiest to work with? 48 kilometers, since 48 is the least common multiple of 16 and 24.
Filling in the table.
Now we can put constants in the cells for leg lengths as well as in some of the cells for rates.
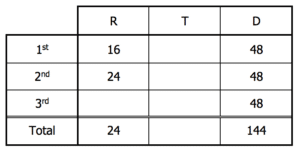
We can also determine a time for the bottom row—a combined time for all three legs—by dividing the combined distance by the average rate.
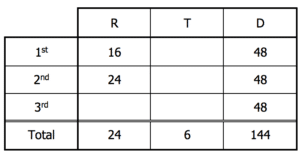
That allows us to determine the time for the third leg, since the sum of the times for the three legs is the combined time for the tour.
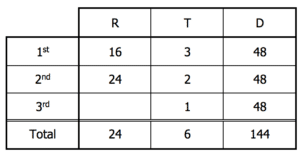
Finally, we can determine the rate for the third leg by dividing the distance by the time.
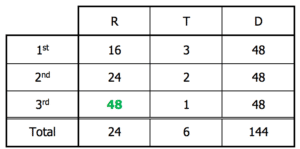
The little shortcut.
The little shortcut isn’t as powerful as the big one, and it’s peculiar to average problems, so you won’t get much use out of it, but here it is.
Since the rate for the second leg is equal to the average rate, we can ignore that leg. Because Div averages 24 kph for the entire tour and 24 kph for the second leg, he must also average 24 kph for the balance of the tour. So we could leave the second leg out altogether.
What would the RTD table for that amended problem look like? Well, if we use the big shortcut, we’ll still probably make each leg 48 kilometers, since 48 is the least common denominator of the rate in kph of the first leg and the rate in kph of the entire tour.
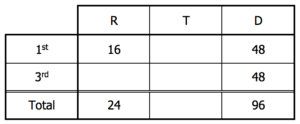
We can complete the top and bottom rows by dividing distance by the time.
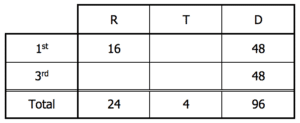
Next, we can complete the “time” column.
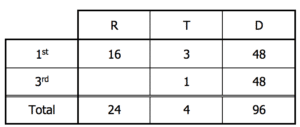
Finally, we can divide the length of the third leg, 48 kilometers, by the time for the third leg, 1 hour, to determine the rate for the third leg.






Leave a Reply