My last few blog posts have involved rate problems about simultaneous movement. In each of these problems we discovered exactly two travelers who either (1) moved at their own constant rates for the entire time period covered by the story, or (2) moved at their own constant rates and started and stopped simultaneously.
If you’d like to review before moving on, check out my previous posts on the topic:
- Using Diagrams to Solve Rate Problems: Part 1
- Using Diagrams to Solve Rate Problems: Part 2
- A Different Use of the RTD Table: Part 1
- A Different Use of the RTD Table: Part 2
We used the RTD (Rate, Time, and Distance) table to manage these problems, but some test-takers probably found that method to be overkill. Those readers judged that they could translate the problems directly from English to algebra without benefit of any table.
Today I’m going to give you a more complicated problem, one in which the travelers don’t move simultaneously:
Jan’s house and Cindy’s house are joined by a straight road 24 miles long. Jan and Cindy agree to meet at a restaurant along that road, twice as far from Jan’s house as from Cindy’s. Beginning at noon, Cindy walks to the restaurant at a constant speed of 3 miles per hour. Later, Jan drives to the restaurant at a constant speed of 30 miles per hour. If they arrive at the restaurant simultaneously, at what time did Jan begin her drive?
A) 12:32
B) 1:25
C) 1:52
D) 2:08
E) 2:40
This is likely to be a frustrating problem. The algebra—if we can get to the algebra—probably won’t be too complicated, but the translation into algebra looks daunting, if only because we haven’t likely seen a very close model of this problem before. Let’s try our good friend the RTD table, and see if it eases the translation.
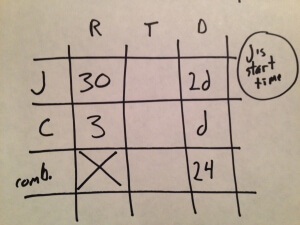
We’ll set the table up as we have before, with columns for rate, time, and distance, and with rows for Jan, Cindy, and their combined distance:
Rates.
We’re given Jan’s and Cindy’s rates directly, so let’s put those in.
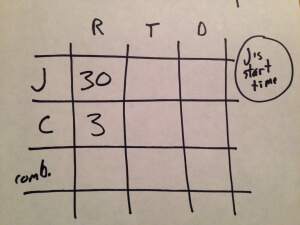
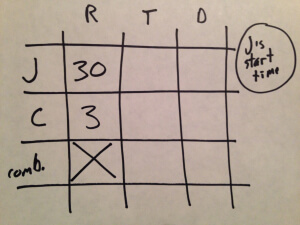
Distance.
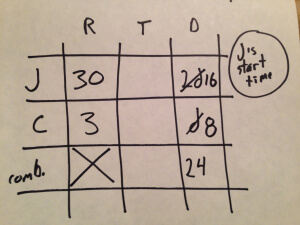
We are given the combined distances for Jan and Cindy, 24 miles, so we can include that. We’re told that the restaurant is “twice as far from Jan’s house as from Cindy’s.” If we call the distance from Cindy’s house d, then the distance from Jan’s house must be 2d.
d+2d=24
3d=24
d=8.
So the restaurant is 8 miles from Cindy’s house and 16 miles from Jan’s.
Time.
Let’s complete the rows for Cindy and Jan. Since we know that Cindy’s rate is 3 mph and that her distance is 8 miles, we can conclude that her time was 8/3 hours. Since we know that Jan’s rate is 30 mph and that her distance is 16 miles, we can conclude that her time was 16/30 hours.
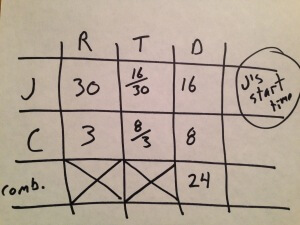
But now what? Well, if Cindy took 8/3 of an hour, then she took hours, or 2 hours and 40 minutes. Since she started at noon, she arrived at the restaurant at 2:40.
Since Cindy and Jan arrived simultaneously, Jan too arrived at 2:40. At what time did she leave? Well, she took 16/30 of an hour. That’s 32/60, or 32 minutes. Since she arrived at 2:40 after 32 minutes of travel, she must have started her drive at 2:08.
Could we do this without the RTD table?
If you’ve read my other blogs on the use of this table, then you know that the answer is “yes,” at least for some people. The table is an aid to translation, and a few people are able to translate even very complicated rate problems directly into algebra without benefit of the table.
Still, I think that the RTD table is especially useful for this problem, even though as we used it here it turned out to just be two equations stacked one on the other, and even though it left us with a fair bit of work still to do. Disciplined well-practiced use of the RTD table allows us to chip away at the familiar parts of the problem and to reserve our cognitive resources for the less familiar parts.






Leave a Reply