My last several posts have been devoted to the use of a table to answer rate problems. Today’s post will assume familiarity with that table, so please take a look back at these posts is you’re not already familiar with the RTD table:
- Using Diagrams to Solve Rate Problems: Part 1
- Using Diagrams to Solve Rate Problems: Part 2
- A Different Use of the RTD Table: Part 1
- A Different Use of the RTD Table: Part 2
- Using the RTD Table for a Complicated Problem
Here’s today’s problem:
Div’s bicycle tour consists of three legs of equal length. For the first leg Div averaged 16 kilometers per hour. For the second leg he averaged 24 kilometers per hour. What speed must Div average for the final leg in order to average 24 kilometers per hour for the entire tour?
A) 20 kilometers per hour
B) 28 kilometers per hour
C) 32 kilometers per hour
D) 40 kilometers per hour
E) 48 kilometers per hour
WARNING!
I usually start with the bare outline of an RTD table, and then fill it in bit-by-bit. Today, though, I’m going to start with a warning. Every problem on average rates has at least one attractive wrong answer that is intuitively appealing and seems promise a quick solution. Can you spot it here?
You might have said 20 kilometers per hour, because that is the average of the given rates, 16 and 24 kilometers per hour. Fair enough. That is wrong and will attract some people who read too quickly. I’m more concerned about a different trap, though.
Average-rate problems encourage you to assume that spending the same distance at two (or more) different rates allows you simply average those rates. For instance, in this problem, we might suppose that traveling one leg at 16 kph, one at 24 kph, and one at 32 kph would yield an average speed for the whole tour of 24 kph, because 24 is the simple mean of 16, 24, and 32 . And there’s 32 kilometers per hour waiting for you!
In fact, though, speeds are weighted according to how much time you spend at each, not how much distance you spend at each. This means that average speeds are generally less than you’d guess based on their component speeds, since it takes you more time to travel a given distance when you travel it slowly. (This neat fact deserves a post of its own, and I’ll write one soon.)
As a practical matter, what this means for average speed problems is that you will usually need to approach them not as simple averages or even as weighted averages. Instead, you need to view average speed problems through this formula:
Back to the RTD table!
Let’s devote one row of the table to each leg, and a fourth row to the total.
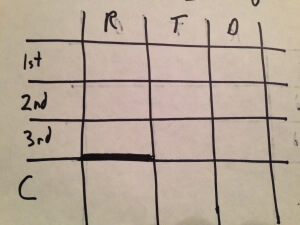
For an average-rate problem, you’ll need a wall between the rates of the various legs and the rate for the whole trip. I’ve represented that wall by drawing a heavy black line above the bottom-left cell. The only way to fill in that cell is from the other information in the bottom row, not directly from the cells above it in the same column.
The red lines below show the direction in you will usually add each of the columns and divide the bottom row.
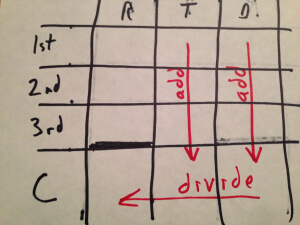
Today’s problem is a bit strange though, so we’ll do things in a slightly different way.
Rate.
Okay, let’s get rid of those red lines and add the rate information we’ve been given: the rates for the first two legs and the average rate.
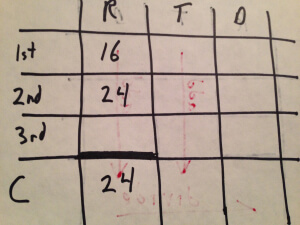
Distance.
Those are the only constant values we’ve been given, but we can add a little more information even so. We don’t know the distance, but we know that it’s the same for every leg, so let’s call that distance d, and then sum the legs to get a combined distance.
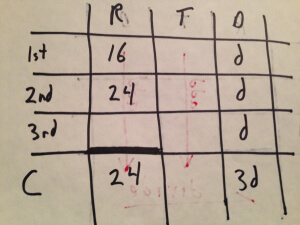
Time.
Now that we’ve represented both rate and distance for three of our four rows, we can determine times for those rows by division; ![]()
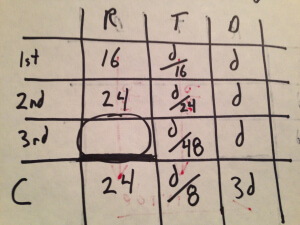
Back to time.
Notice that the column for “time” is almost complete. Since the total time, d/8, must be the sum of the other times, we can determine the missing time for the third leg.
Multiply through by 48, the least common denominator.
Transpose.
Divide.
Let’s add that to the table.
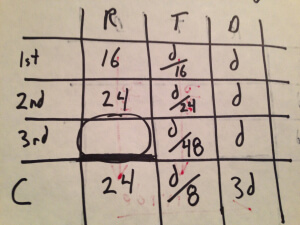
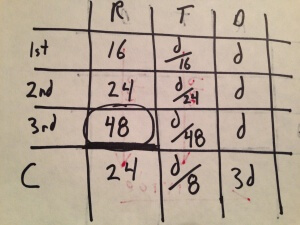
Finally our answer!
Now that we have the distance and time for the third leg, we can divide to determine the rate;
![]()
Okay, even using the RTD table, we still had to do an awful lot of work. It turns out, though, that a couple of shortcuts could have saved us most of that work. Come back tomorrow to see how.



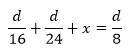




Leave a Reply