This is the third in a series of probability articles for the GMAT Quantitative Section. In the first, I discussed the “AND” and “OR” rules for probability. In the second, I discussed the “complement rule” and how to use this to solve “at least” problems in probability. For a warm-up, here are some challenging GMAT Problem Solving problems on probability.
1) Five children, Anaxagoras, Beatrice, Childeric, Desdemona, and Ethelred, sit randomly in five chairs in a row. What is the probability that Childeric and Ethelred sit next to each other?
-
- (A) 1/30
-
- (B) 1/15
-
- (C) 1/5
-
- (D) 2/5
- (E) 7/20
2) A division of a company consists of seven junior-level employees and five managers. If two of these twelve employees are randomly selected as representatives of the division, what is the probability that both representatives will be a manager?
-
- (A) 1/6
-
- (B) 2/5
-
- (C) 2/9
-
- (D) 5/12
- (E) 5/33
3) John has on his shelf four books of poetry, four novels, and two reference works. Suppose from these ten books, we were to pick two books at random. What is the probability that we pick one novel and one reference work?
-
- (A) 1/2
-
- (B) 2/5
-
- (C) 3/10
-
- (D) 7/20
- (E) 8/45
Do these problems make your head spin? Then you have found just the post you need!
Probability and counting
Fundamentally, the definition of probability is
The previous two posts talked about various tricks for calculating probabilities in different scenarios, but in some problems, we just have to count the numbers in the numerator and the denominator. This means, we need to understand basic counting techniques, including combinations and permutations. The details of the counting techniques are explained in these posts. Any probability problem involving counting is really two counting problems in one—we have to calculate the denominator, the number of all possible cases, and the numerator, the number of only those cases that meet the condition specified. I’ll just mention that often, the most challenging part of any counting problem, especially for special cases (e.g. the numerators of these probability expressions) is how we frame the problem. Details of this process will be explained below in the solutions to problems.
Summary
If counting techniques are unfamiliar to you, read those two other posts. Once you feel confident with counting techniques, give the problems above another try before reading the solutions below. In the last article in this series, I will discuss a special case of probability problems on the GMAT: geometric probability.
Practice problem explanations
1) First, we will count all the possible arrangements of the five children on the five seats, all the possible orders. This is 5! = 120. That’s the denominator.
Now, the more challenging part: we have to figure out how many arrangements there are involving C & E sitting together. This is a tricky problem to frame, so I’ll demonstrate the steps to follow. First, let’s look at the seats these two could be next to each other. There are four possible pairs of seats in which they could be next to each other
i. X X _ _ _
ii. _ X X _ _
iii. _ _ X X _
iv. _ _ _ X X
In each of those four cases, we could have either CE or EC, either order, so that’s 4 x 2 = 8 ways we could have just C & E sitting next to each other with the remaining three seats empty.
For the final step, we need to consider the other three children, A & B & D. In each of the eight cases, there are three blank seats waiting for those three, and those three could be put in any order in those blank seats. Three elements in any order—that’s 3! = 6. Thus, the total number of arrangements in which C & E would be next to each other would be 8 x 6 = 48. This is our numerator.
The probability would be this number, 48, over the total number of arrangements of the children, 120.
Answer = D
2) First, the denominator. We have twelve different people, and we want a combination of two selected from these twelve. We will use the formula:
which, for profound mathematical reasons we need not address here, is also the formula for the sum of the first (n – 1) positive integers. Here
That’s the total number of pairs we could pick from the twelve employees. That’s our denominator.
For the numerator, we want every combination of two from the five employees who are managers. That’s
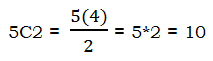
That’s the number of pairs of managers we could pick from the five. That’s our numerator.
Answer = E
3) For the denominator, we are going to pick two books from among ten total: a combination of two from ten. Again, we will use the formula:
which, for profound mathematical reasons we need not address here, is also the formula for the sum of the first (n – 1) positive integers. Here
That’s the total number of pairs of books we could pick from the ten on the shelf. That’s our denominator.
Now, the numerator. We want one novel and one reference work. Well, there are four novels and two reference works, so by the FCP, the number of ways we can pick this is 4 x 2 = 8. That’s the total possible number of pairs involving exactly one of these four novels and exactly one of these two reference works. That’s our numerator.
Answer = E


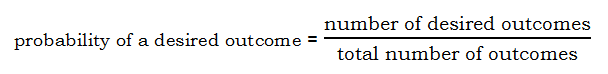
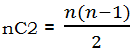

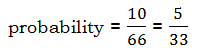
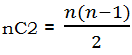
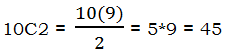





Leave a Reply