Here are four practice problems involving similar figures.
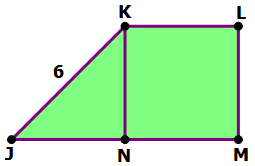
1) In the figure, KLMN is a square, and angle KJN = 45°. Find the area of figure JKLMN.
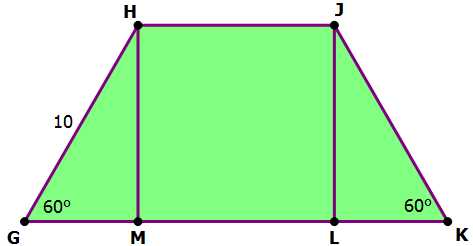
2) In the diagram, HJLM is a square, and GH = 10. Find the area of trapezoid GHJK.
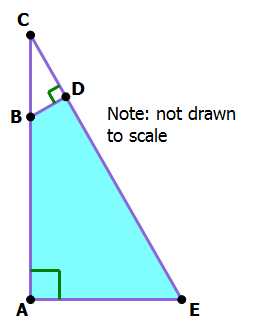
3) In the diagram, BD = 5, CD = 10, and AE = 40. What is the area of the shaded region?
-
(A) 175
(B) 350
(C) 775
(D) 1150
(E) 1575
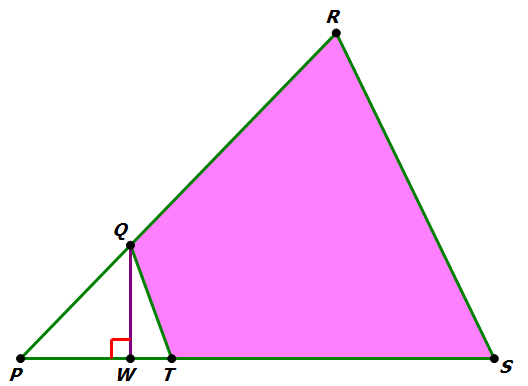
4) In the figure above, angle PTQ = angle QRS = 70º, PT = 4, PR = 12, and the shaded region has an area of 48. What is the length of QW?
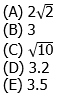
Answer will appear at the end of this blog.
Geometric similarity
Two geometric figures are similar if they have the same shape but are difference sizes. One is a smaller or larger version of the other. Similar figures always have all the same angles, and their sides are proportional. Some previous blog with relevant materials are
1) The GMAT’s Favorite Triangles: the 30-60-90 triangle and the 45-45-90 triangle
2) Similar Shapes, including scale factor
3) Scale Factors and Percent Increase/Decrease
You definitely need to know the two special right triangles in #1, and other blogs contain many time saving hints.
Practice problem explanations
1) Since KN must be perpendicular to JM, we know that JNK must be a 45-45-90 triangle. The legs are equal, and the hypotenuse is the square root of 2 times larger than either leg. Let JN = KN = x. Then
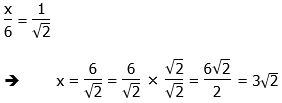
In that work, we rationalized the denominator when we divided by the radical. This number for x is the side of the square, so square KLMN has an area which is this number squared.
That’s part of the area. Now, notice that triangle JKN would be equivalent to a square of the same size cut in half along the diagonal. This triangle must have exactly half the area of the square. Well, the square is 18, so the triangle must be 9, and together, they must have an area of 27.
Answer = (E)
2) This entire problem hinges on recognizing that triangles GHM and JKL are 30-60-90 triangles and using the properties of those triangles. First of all, notice that because HJLM is a square, it must be true that HM = JL. This means, the two triangles, GHM and JKL, must be congruent and have all the same sides & angles. GH = JK = 10.
Now, in a 30-60-90 triangle, the smaller leg is half the hypotenuse, so GM = LK = 5. The longer leg is the square root of 3 times the shorter leg, so
This is the side of the square, so we square this to get the area of square HJLM.
That’s part of the area. Now, we need the area of the triangles. One triangle is A = 0.5bh, so two triangles would simply be A = bh
Answer = (D)
3) In this problem, we need the crucial fact that the ratio of areas is proportional to scale factor squared.
First of all, side BD in BCD corresponds to side AE in ECA. AE:BD = 40:5 = 8, so the scale factor between the two triangles is 8. Every length in triangle ECA is 8 times bigger than the corresponding length in triangle BCD.
This means that the area of ECA is 8 squared, or 64 times bigger than the area of BCD. Well, it’s easy to calculate that BCD has an area of 25. This means that ECA must have area of
25*64 = 50*32 = 100*16 = 1600
Notice, we used the doubling and halving trick in that problem to simplify the multiplication. That’s the area of ECA. Well, the shaded area doesn’t include BCD, so
shaded = (triangle ECA) – (triangle BCD) = 1600 – 25 = 1575
Answer = (E)
4) We know the larger and smaller triangles are similar, because they share the angle at P, and one other angle in each is 70º. What’s tricky is that they have different orientations, so that side PT actually corresponds to side PR. We know PR:PT = 3, so that’s the scale fact. Every length in triangle PRS is three times more than the corresponding side in triangle PTQ. If lengths are multiplied by 3, area is multiplied by 3 squared, or 9. Let’s say that the area of triangle PTQ is A. Then the area of triangle PRS is 9A. The shaded area is the difference of the two triangle areas, or 8A. If 8A = 48, this means A = 6, and that’s the area of triangle PTQ.
Well, PT = 4 is a base of PTQ, and QW is a corresponding altitude: call its length h.
A = 0.5bh
6 = 0.5(4)h
6 = 2h
3 = h
The length of QW is 3.
Answer = (B)


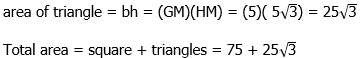



Leave a Reply