Some GMAT students who struggle with geometry find similar shapes confusing. I’ll try to clear that confusion up now. First, though, a couple tricky practice questions involving geometric similarity.
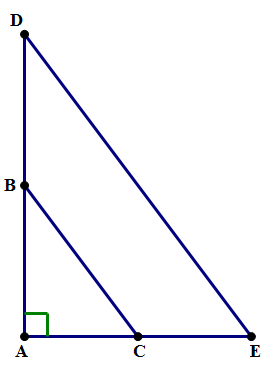
1) In the diagram above, BC is parallel to DE, DE = 20, and AC = CE = 6. What is the length of AB?
-
- (A) 7
-
- (B) 8
-
- (C) 9
-
- (D) 10
- (E) 11
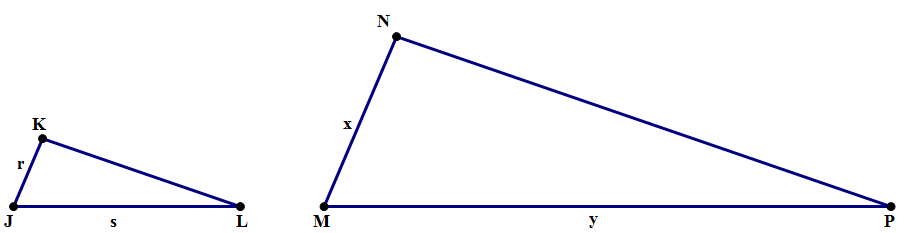
2) In the diagram above, ∠J = ∠M, ∠K = ∠N, and side lengths are as shown. Given this, y must equal
-
- (A) r/sx
-
- (B) x/sr
-
- (C) sr/x
-
- (D) sx/r
- (E) rx/s
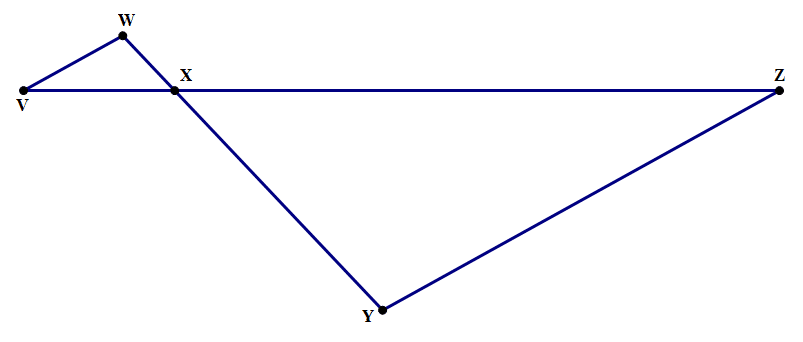
3) In the diagram above, ∠W = ∠Y and VX is one fifth of VZ. If the area of triangle VWX is 5, what is the area of triangle XYZ?
-
- (A) 25
-
- (B) 40
-
- (C) 50
-
- (D) 80
- (E) 125
Geometric Similarity
When two geometric figures are the same shape and same size, they are congruent. You may recall that a great deal of Geometry class is spend proving things are congruent. Once you know they are congruent, there’s not much more mystery — every single piece of one figure is absolutely identical to the corresponding piece of the other figure. They are identical copies of one another.
When two geometric figures are the same shape and different sizes, they are similar. The larger one is a bigger copy of the smaller one. Each is a “scaled up” or “scaled down” version of the other. All the lengths will be different, but all the angles will be the same. Having all the same angles means the same as being geometric similar.
In fact, for triangles, there’s a great shortcut. Suppose two angles of one triangle equal two angles of another triangle —- the third angles would also have to be equal, by the whole add-to-180° thing, so we don’t even need to consider them — if two angles of one triangle equal two angles of another triangle, that’s enough to prove the triangles similar. From this fact alone, it should be clear that there are similar triangles in all three problems above.
The similar geometric shapes don’t have to be triangles. All squares are similar. All regular octagons are similar. All circles are similar. We can’t say that all rectangles are similar, because rectangles come in an infinite assortment of different shapes, different ratios; nevertheless, if we pick one particular kind of rectangle, say, the Golden Rectangle, then we could say: all Golden Rectangles are similar.
The sides and proportionality
If two figures are geometrically similar, one is larger and one is smaller, so the lengths do not stay the same. BUT, there’s a remarkable relationship among the lengths: the lengths of similar figures are proportional.
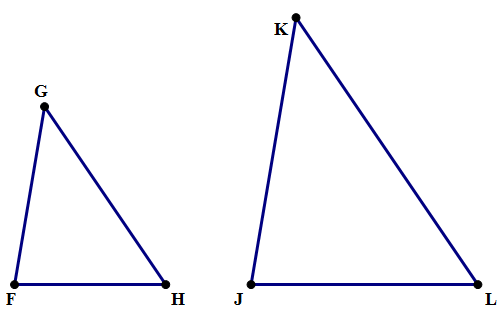
What does it mean to say they are “proportional”? That means we can set up a proportion, that is, an equal with a fraction on either side. The ratio of sides in one figure must equal the ratio of corresponding sides in the other figure. For example, suppose, in the figure below, we are given ∠F = ∠J and ∠G = ∠K.
That’s enough to establish the two triangles are similar. This, in turn, allows us to deduce the following proportions involving the lengths.
We could also take the reciprocal of both sides in any of those, or cross-multiply any of those and re-arrange in several ways. Ratios and proportions give you a ton of information for problem-solving!
Scale factor
Another way to think about the proportionality of similar figures has to do with scale factor — how many times bigger or smaller we make the second shape. If use the letter k to denote scale factor, then we can find k by finding the ratio of any two corresponding sides. Still referring to the diagrams of triangles FGH & JKL above, we could say
In other words, if you can figure out the ratio of any pair of corresponding lengths, you automatically know the ratio of all the other corresponding lengths!
Similarity and Area
When two figures are similar, each length in one is the scale factor, k, times the corresponding length in the other. Lengths get multiplied by k. Well, if you think about area, every area formula on the planet involves the product of two lengths. It may be one length squared, but even that’s a length times a length. There may be other factors, 1/2 or 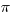 or something like that, but there’s always a product of two lengths. This means that if we know the area of the first figure, computed from the lengths in that first figure, then all the lengths in the second figure are multiplied by k. Since each length used to calculate the area of the second figure is multiplied by k, the area itself is multiplied by k*k, or
or something like that, but there’s always a product of two lengths. This means that if we know the area of the first figure, computed from the lengths in that first figure, then all the lengths in the second figure are multiplied by k. Since each length used to calculate the area of the second figure is multiplied by k, the area itself is multiplied by k*k, or 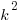 . This is a big idea: lengths are multiplied by k, and areas are multiplied by
. This is a big idea: lengths are multiplied by k, and areas are multiplied by 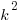 . This has important implications in percent increase problems involving similar figures.
. This has important implications in percent increase problems involving similar figures.
Summary
Geometric similarity involves a web of interconnected ideas that afford the folks who write the GMAT a virtually unlimited playground of possible questions. If you master the ideas in this post, you will know everything you need to know about this rich topic. Now that you’ve read, take another look at the practice questions, before moving on to the explanations below.
Explanations to the practice questions
1) From the fact that the two segments are parallel, we know that ∠ACB = ∠E and ∠ABC = ∠D. The triangles ABC and ADE have all the same angles, so they are similar. Since AC = 6 and AE = 12, we know the scale factor is k = 2 —– if C is the midpoint of AE, that means B must be the midpoint of AD. Since DE = 20, we know BC must be half of this — BC = 10. With this and AC = 6, we can use the Pythagorean Theorem in the smaller triangle, triangle ABC. In fact, if you remember your Pythagorean Triplets, we don’t even have to do a calculation — if we multiply the fundamental {3, 4, 5} triplet by 2, we get {6, 8, 10} — since AC = 6 and BC = 10, this must mean AB = 8.
Answer = B
2) This is a straight question about the proportions of sides in similar triangles. From the angle information, we know the two triangles are similar. This means
Answer = D
3) This is a tricky one. Because ∠W = ∠Y and because the two vertical angles at point X, ∠WXV and ∠ZXY, must be equal, this is enough to establish the triangles are similar. The next fact is fascinating: “VX is one fifth of VZ.” If VZ is “five parts”, then VX is “one part”, and this means XZ would be “four parts” —- that means the scale factor k = 4. If k = 4, then areas are multiplied by 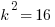 . The area of triangle VWX = 5, so the area of triangle XYZ must be 16 times this —- 16*5 = 80.
. The area of triangle VWX = 5, so the area of triangle XYZ must be 16 times this —- 16*5 = 80.
Answer = D


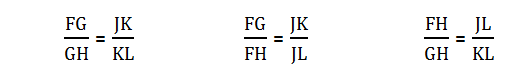
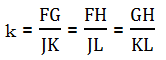
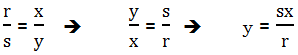




Leave a Reply