How to Solve GMAT Motion Problems

Word Problems make up a majority of the quantitative section of the GMAT (almost 60 percent). Of the word problems they’ll face, students tend to need the most help with GMAT motion problems. This type of problem centers around the “dust” formula, which is short for Distance equals Speed multiplied by Time, or \(\text{D}\times\text{S}=\text{T}\). But there are many varieties of motion problem, and we will discuss techniques for each of them. At the end of this article, you’ll also find motion word problems with solutions for you to test your knowledge!

 

GMAT Motion Problems: Table of Contents

• The Distance Equation
• Multi-Segment Motion Problems
• Average Speed
• Multiple Traveler Questions
• Shrinking and Expanding Gaps
• Data Sufficiency
• GMAT Motion Problems Review: Practice Problems

 

The Distance Equation

Like we mentioned above, Distance equals Speed multiplied by Time, or \(\text{D}\times\text{S}=\text{T}\). If you learn this basic equation well, you’ll be able to dust your math troubles away! (Insert rimshot.)

 
We can rearrange this formula to determine that Speed is equal to Distance divided by Time.

And Time is equal to Distance divided by Speed.

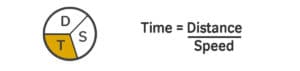
• Distance is the measurement of how far apart objects, people, or points are.
• Speed is the rate at which someone or something is traveling.
• Time is how long it takes to travel.

 
Let’s demonstrate this. Walking at a constant rate of 160 meters per hour, Monroe can cross a bridge in 2 hours. What is the length of the bridge?
 
Here, the length of the bridge is the distance Monroe must cross. Using Distance equals Speed multiplied by Time, we get:
 
\((160\text{meters per hour})\times(2\text{hours})=320\text{meters}\)
 
Seems simple enough so far, right? Let’s check out a few more GMAT motion problems.

 

Multi-Segment GMAT Motion Problems

Oftentimes one traveler will be dividing their trip into multiple segments. In these situations, you need a separate “dust” equation for each segment. You will usually have two equations, which requires a two-variable system of equations to solve. You will often perform substitution.
 
Let’s try this out. Julianne drives the first 360 miles of a trip at 60 miles per hour. How fast does he have to drive, in miles per hour, on the final 210 miles of the trip if the total time of the trip is to equal nine hours?
 
First, we identify all of our parameters. We will call the variables for the first leg of the trip distance D₁, speed S₁, and time T₁; we’ll call the variables for the second leg D₂, S₂, and T₂.
 
From the given information, we know that
 
\(\text{D}_1=360\text{miles}\text{S}_1=60\text{miles per hour}\text{D}_2=210\text{miles}\)
 
\(\text{T}_1=\frac{\text{D}_1}{\text{S}_1}\)
 
\(\text{T}_1=\frac{360\text{miles}}{60\text{miles per hour}}=6\text{hours}\)
 
Because the total time of the trip is to equal nine hours, T₂ must equal nine minus T₁ hours.
 
\(\text{T}_2=3\text{hours}\)
 
\(\text{S}_2=\frac{\text{D}_2}{\text{T}_2}\)
 
\(\text{S}_2=\frac{210\text{miles}}{3\text{hours}}=70\text{miles per hour}\)

 

Average Speed

As we discussed previously, Speed is equal to Distance divided by Time. Let’s take that a step further and talk about average speed. Average speed is defined as total distance traveled divided by the total time period spent traveling. This means that if you have a trip with multiple segments, you’ll want to take the sum of the distances of each segment and divide that by the sum of the times of each segment. Average speed captures the constant speed needed to travel the total distance in the total time.
 
Let’s demonstrate this. Koki drove 16 miles in 10 minutes, and then drove an additional 6 miles in 5 minutes. What is Koki’s average speed for the entire trip in miles per hour?

Click here for the answer and explanation

Well, average speed is the total distance divided by the total time.
 
\(\text{D}_\text{Total}=16\text{miles}+6\text{miles}=22\text{miles}\)
 
\(\text{T}_\text{Total}=10\text{minutes}+5\text{minutes}=15\text{minutes}\)
 
\(\text{S}_\text{Average}=\frac{\text{D}_\text{Total}}{\text{T}_\text{Total}}\)
 
\(\text{S}_\text{Average}=\frac{22\text{miles}}{15\text{minutes}}\times\frac{60\text{minutes}}{1\text{hour}}=88\text{miles per hour}\)

 
That’s straightforward enough, but what if we are not given any distances or times? It is possible to solve an average speed problem, even if all you are given are the different speeds in each segment of the trip. You might then think that average speed would just be the average of all of the speeds, but that is not correct.
 
Let’s say that Nathaniel drove from Gwenville to Samton at an average speed of 24 miles per hour. He then drove the same route on the return trip back from Samton to Gwenville at an average speed of 36 miles per hour. If you were asked to find Nathaniel’s average speed, it would not just be 30 miles per hour (the average of 24 and 36).

Click here to work through this problem

To see this, let’s go back to our MVP dust formula. Since there are two legs of the trip, we will have two equations. D₁, S₁, T₁; D₂, S₂, T₂. Because Nathaniel’s trip is a round trip, we can assume that D₁and D₂ are the same, so we will set both of them equal to D.
 
\(\text{D}_1=\text{D}\text{S}_1=24\text{miles per hour}\text{T}_1=\frac{D}{24\text{miles per hour}}\)
 
\(\text{D}_2=\text{D}\text{S}_2=36\text{miles per hour}\text{T}_2=\frac{D}{36\text{miles per hour}}\)
 
\(\text{D}_\text{Total}=\text{2D}\)
 
\(\text{T}_\text{Total}=\frac{D}{24\text{miles per hour}}+\frac{D}{36\text{miles per hour}}\)
 
\(\text{S}_\text{Average}=\frac{\text{D}_\text{Total}}{\text{T}_\text{Total}}\)
 
\(\text{S}_\text{Average}=\frac{\text{2D}}{\frac{D}{24\text{miles per hour}}+\frac{D}{36\text{miles per hour}}}\)
 
We can factor a D out of this \fraction.
 
\(\text{S}_\text{Average}=\frac{2}{\frac{1}{24}+\frac{1}{36}}\text{miles per hour}\)
 
We can find a common denominator between 24 and 36.
 
\(\text{S}_\text{Average}=\frac{2}{\frac{3}{72}+\frac{2}{72}}\text{miles per hour}\)
 
\(\text{S}_\text{Average}=\frac{2}{\frac{5}{72}}\text{miles per hour}=\frac{2}{1}\times\frac{72}{5}=\frac{144}{5}\text{miles per hour}=28.8\text{miles per hour}\)

 
In summary, whenever you want to find the average speed of a round trip, and you are given the two segment speeds, you can put it in the form \(\text{S}_\text{Average}=\frac{\text{2}}{\frac{1}{\text{S}_1}+\frac{1}{\text{S}_2}}\). You can also use this formula to find one of the segment speeds, given the other segment speed and the average speed.

 

Multiple Traveler Questions

As we discussed in the last section, when one traveler divides their trip into multiple segments, you will need a separate “dust” equation for each segment.
 
Similarly, when we have multiple travelers, we need a separate “dust” equation for each traveler. And, like in the last segment, we will need a system of equations for these problems, too, since the two travelers will have some relationship to each other in distance, speed, and/or time.
 
Let’s demonstrate this. Car X and Y are traveling from A to B on the same route at constant speeds. Car X is initially behind Car Y, but Car Y’s speed is 0.8 times Car X’s speed. Car X passes Car Y at noon. At 1:45 pm, Car X reaches B, and at that moment, Car Y is still 35 miles away from B. What is the speed of Car X in miles per hour?

Click here for the answer and explanation

Like last time, we’ll start by defining our parameters: D_X, S_X, T_X, and D_Y, S_Y, T_Y. We’ll consider the point at which Car X passes Car Y to be our initial time, and we’ll consider the point at which Car X reaches B to be our final time. This means that both T_X and T_Y are one hour and 45 minutes, or 1.75 (\(\frac{7}{4}\)) hours.
 
In that timeframe, Car X travels all the way to B, but Car Y is still 35 miles away from B.
\(\text{D}_\text{X}=\text{D}\text{D}_\text{Y}=\text{D}-35\)
 
Car Y’s speed is 0.8 (\(\frac{4}{5}\)) \times Car X’s speed.
 
\(\text{S}_\text{Y}=\frac{4}{5}\times\text{S}_\text{X}\)
 
Now we have defined all of our parameters; let’s set up the two equations.
 
Car X: \(\text{D}=\text{S}_\text{X}\times(\frac{7}{4}\text{hour})\)
 
Car Y: \(\text{D}-35=\frac{4}{5}\times\text{S}_\text{X}\times(\frac{7}{4}\text{hour})\)
 
We can substitute the D in Car X’s equation into Car Y’s equation.
 
\((\text{S}_\text{X}\times(\frac{7}{4}\text{hour}))-35=\frac{4}{5}\times\text{S}_\text{X}\times(\frac{7}{4}\text{hour})\)
 
Multiply \(\frac{4}{5}\) by \(\frac{7}{4}\).
 
\(\frac{7}{4}\text{S}_\text{X}-35=\frac{7}{5}\text{S}_\text{X}\)
 
\(\frac{7}{4}\text{S}_\text{X}-\frac{7}{5}\text{S}_\text{X}=35\)
 
\(\frac{35}{20}\text{S}_\text{X}-\frac{28}{20}\text{S}_\text{X}=35\)
 
\(\frac{7}{20}\text{S}_\text{X}=35\)
 
\(\frac{20}{7}\times\frac{7}{20}\text{S}_\text{X}=\frac{35}{1}\times\frac{20}{7}\)
 
\(\text{S}_\text{X}=100\text{miles per hour}\)

 

 

Shrinking and Expanding Gaps

Imagine that you see your friend in the park after the pandemic is over. If you start excitedly running towards each other, you would reach each other faster than you would if your friend had remained stationary. If instead you run away from each other, the distance between you would grow faster than if one of you had remained stationary. In both cases, the two of you are traveling in opposite directions, and your combined speed is faster than each of your separate speeds.
 
Now, imagine that you start running toward your friend, but your friend turns around and runs away from you. You would catch your friend more slowly than you would if your friend had remained stationary. And if you passed your friend after catching up to them, it would take you longer to grow your lead than if they had stopped running. In both cases, the two of you are traveling in the same direction, and your combined speed would be slower than each of your separate speeds.
 
In each of these scenarios, there is a gap between you and your friend that is either shrinking or expanding. If two bodies are traveling in opposite directions, you need to add their speeds together to find their gap speed. The gap speed is faster than each of the separate speeds. If they are traveling in the same direction, you need to take the positive difference of the speeds. The gap speed is slower than each of the separate speeds.
 
Instead of using two separate “dust” equations for two different travelers, you can just use one for the shrinking or expanding of the gap between the travelers. The distance is the length of the gap, the time is how long it takes for the gap to fully shrink or expand, and the speed is either the sum or the difference of the two travelers’ speeds, depending on their respective directions. This technique can greatly simplify and expedite problems like these. To help you keep track of all the parameters in the problem, you can use a diagram.
 
Let’s say that a car and truck are moving in the same direction on the same highway. The truck is moving at 50 miles an hour, and the car is traveling at a constant speed. At 3 pm, the car is 30 miles behind the truck and at 4:30 pm, the car overtakes and passes the truck. What is the speed of the car?

Click here for the answer and explanation

The car and truck are moving in the same direction, and the car is gaining on the truck. This means that the gap between the vehicles is shrinking and that the gap rate is the difference of the two vehicles’ respective speeds.
 
\(\text{S}_\text{G}=\text{S}_\text{C}-\text{S}_\text{T}\)
 
The distance of the gap is initially 30 miles.
 
\(\text{D}=30\text{miles}\)
 
The time frame we are given for the closing of the gap is from 3 pm to 4:30 pm.
 
\(\text{T}=1.5\text{hours}=\frac{3}{2}\text{hours}\)
 
\(\text{S}_\text{G}=\frac{\text{D}}{\text{T}}\)
 
\(\text{S}_\text{G}=\frac{30\text{miles}}{\frac{3}{2}\text{hours}}=30\times\frac{2}{3}=20\text{miles per hour}\)
 
\(20\text{miles per hour}=\text{S}_\text{C}-50\text{miles per hour}\)
 
\(20\text{miles per hour}+50\text{miles per hour}=\text{S}_\text{C}=70\text{miles per hour}\)

 

 

Data Sufficiency

You may also encounter problem solving in motion in the con\text of a data sufficiency question. These GMAT motion problems may ask you to identify one of the “dust” elements, i.e., distance, speed, or time. To achieve data sufficiency, you will need to have both of the other elements.
 
The question may ask you to determine the average speed of a person making a round trip. Referring back to the round-trip average speed formula, \(\text{S}_\text{Average}=\frac{\text{2}}{\frac{1}{\text{S}_1}+\frac{1}{\text{S}_2}}\), in order to achieve sufficiency, you will need to have the person’s speeds on each leg of their trip.
 
Multiple traveler problems may also be featured in data sufficiency problems. In these situations, just follow the classic data sufficiency rule: you need as many equations as you have unknowns. For example, if you have two travelers, and thus two “dust” equations, you cannot achieve sufficiency unless you only have two unknowns (e.g., distance and speed of one of the travelers.)
 

• How are you doing with these GMAT motion problems? Try your hand at this free data sufficiency question from Magoosh, then review the video explanation.

 

GMAT Motion Problems Review: Practice Problems

OK, now let’s practice! The following GMAT motion problems deals with one or more of the motion topics discussed above. Happy solving!

Let us know how you did on these practice questions in the comments below. If you’re looking for more GMAT motion problems, try out one of Magoosh’s GMAT plans, which comes with practice tests, video lessons, and study schedules. Good luck!