Learn the most common solutions to the Pythagorean Theorem
There aren’t many numbers you need to memorize for success on the GMAT Quantitative section, but knowing a few key Pythagorean triplets will save you a ton of time. First, try these GMAT practice question: remember: no calculator!
1) In right triangle ABC, BC = 48 and AB = 60. Find AC
-
(A) 32
(B) 36
(C) 40
(D) 42
(E) 45
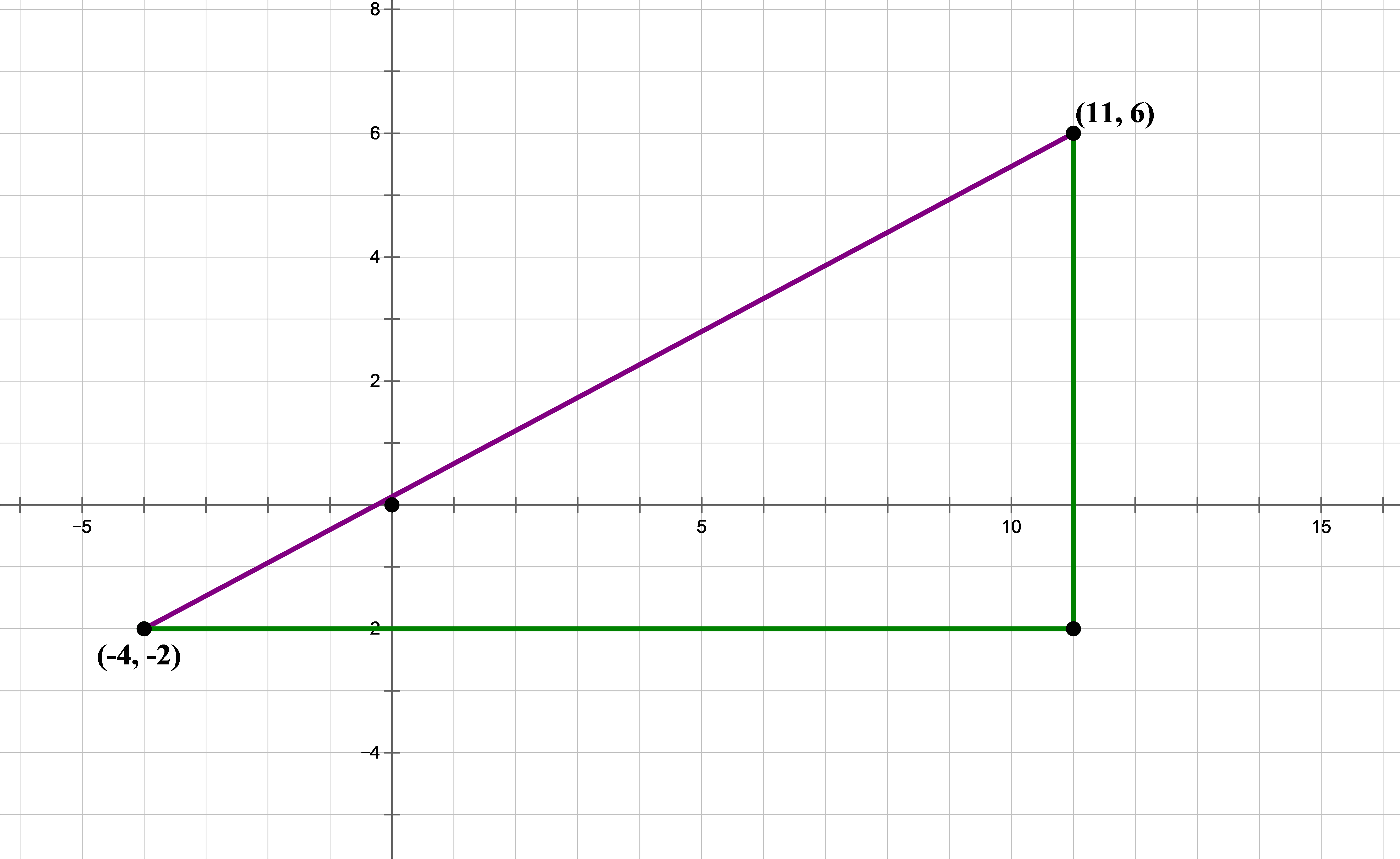
2) In the x-y plane, what is the distance between (-4, -2) and (11, 6)?
-
(A) 16
(B) 17
(C) 18
(D) 19
(E) 20
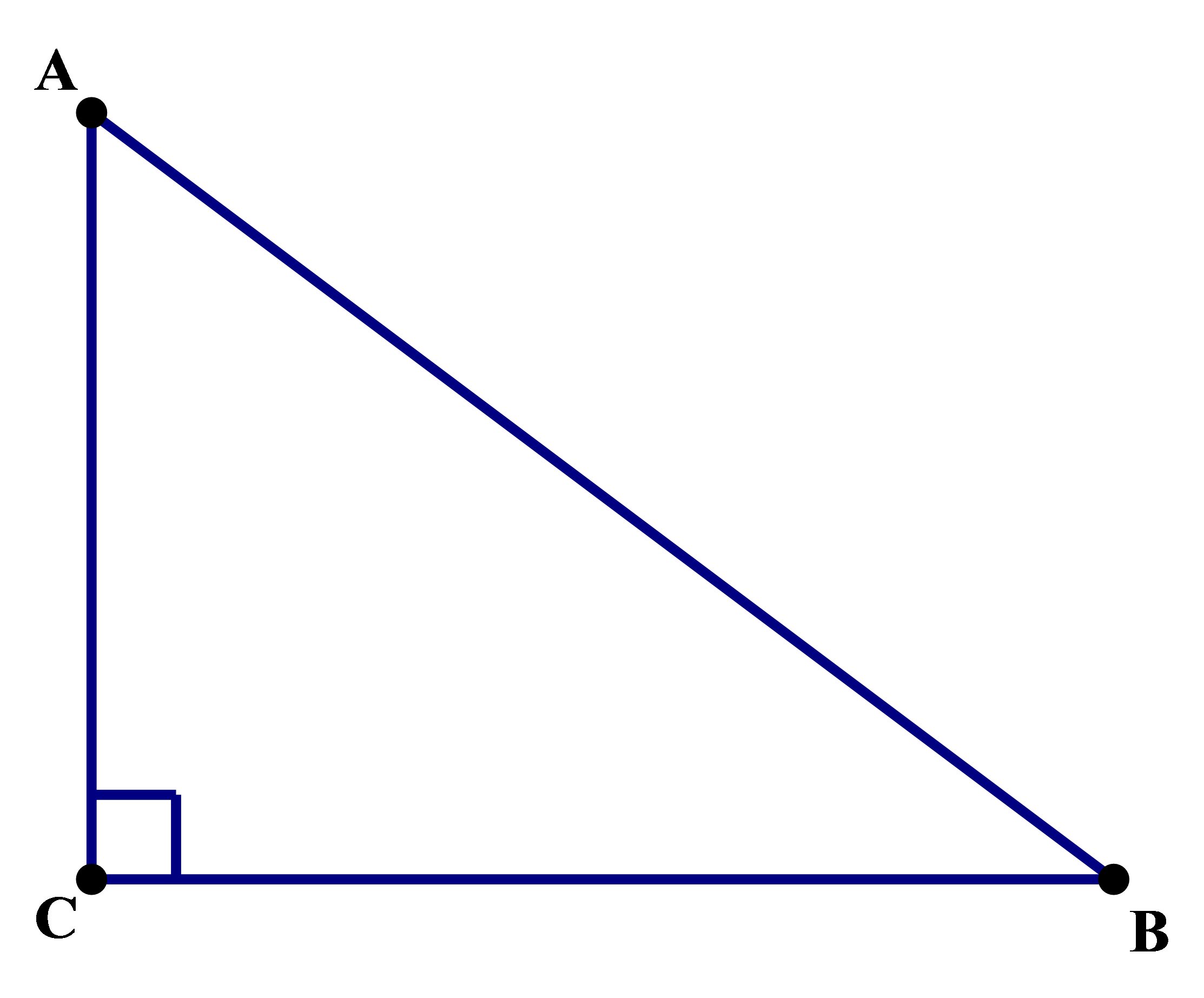
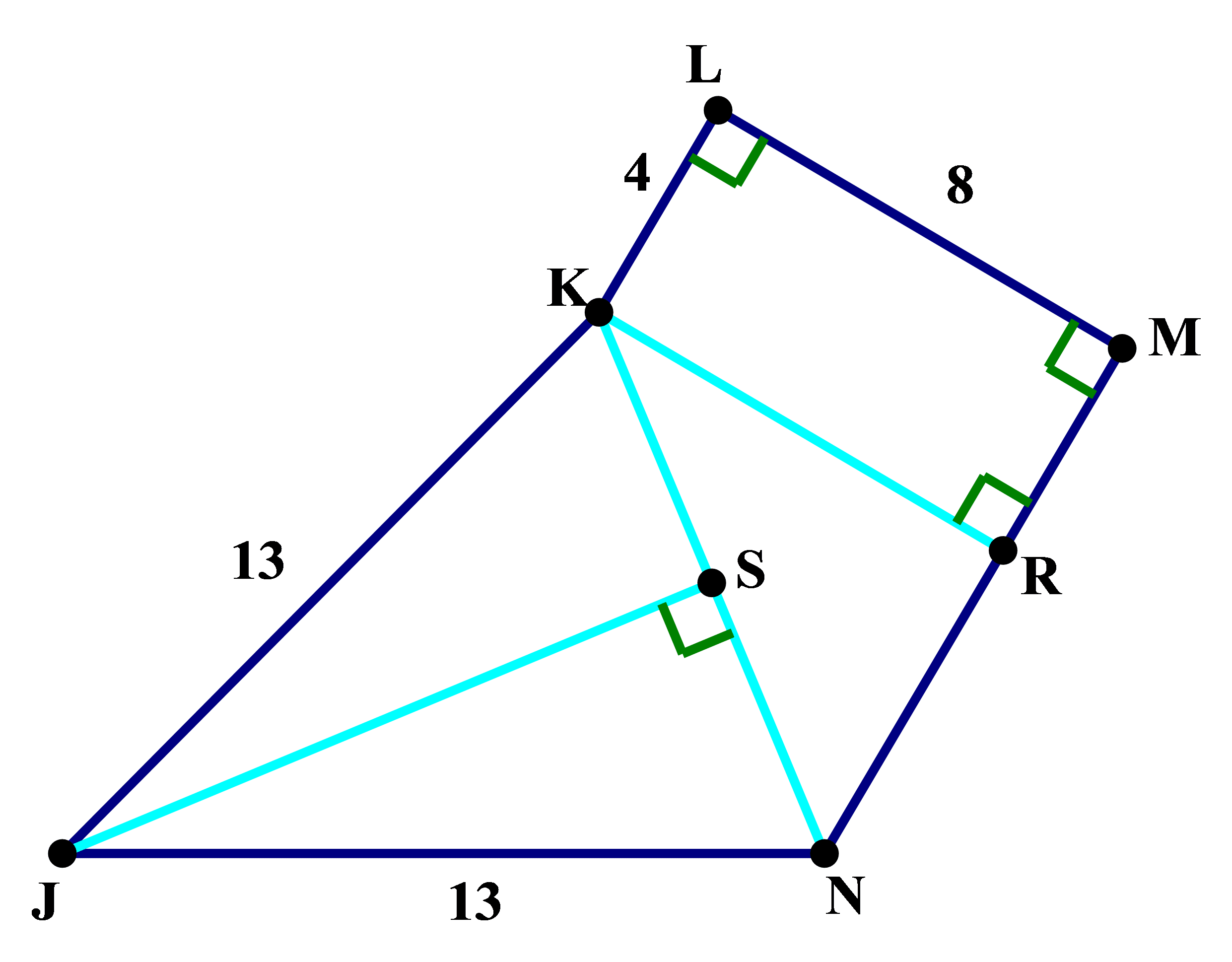
3) In the diagram above, ∠L = ∠M = 90°, KL = 4, LM = 8, MN = 10, and JN = JK = 13. What is the area of JKLMN?
-
(A) 92
(B) 96
(C) 100
(D) 108
(E) 116
Good numbers to memorize
In almost all cases, I will recommend that GMAT student learn to remember mathematical facts without memorizing them. This is one of the few cases in which I will unapologetically recommend memorizing. There are certain sets of positive integers that satisfy the Pythagorean Theorem: these sets of three integers are called Pythagorean triplets. Some of them are very obscure, but some of them are extremely common. The most common by far is the triplet (3, 4, 5). In all of these, I am listing a set (a, b, c) that satisfies 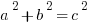 , so the largest number would be the hypotenuse of the triangle. Two other common sets of Pythagorean triplets are (5, 12, 13) and (8, 15, 17). Right there, BAM! Memorize those three sets, and you will spare yourself many stressful moments of lengthy calculations on the GMAT Quantitative section, when you have no calculator.
, so the largest number would be the hypotenuse of the triangle. Two other common sets of Pythagorean triplets are (5, 12, 13) and (8, 15, 17). Right there, BAM! Memorize those three sets, and you will spare yourself many stressful moments of lengthy calculations on the GMAT Quantitative section, when you have no calculator.
First of all, if you encounter a right triangle with legs 8 & 15, you won’t have to square and add things up: rather, you will just know that the hypotenuse is 17. The benefits, though, of that wee bit of memorizing expend wildly when you realize: you can multiply any of those three sets by any integer and get a new set of Pythagorean Triplets. The first set, (3, 4, 5), is the most common to see in multiplies —- (6, 8, 10), (9, 12, 15), (12, 16, 20), etc. —- but once in a while you may see one of the other two multiplied by something small, like 2 or 3.
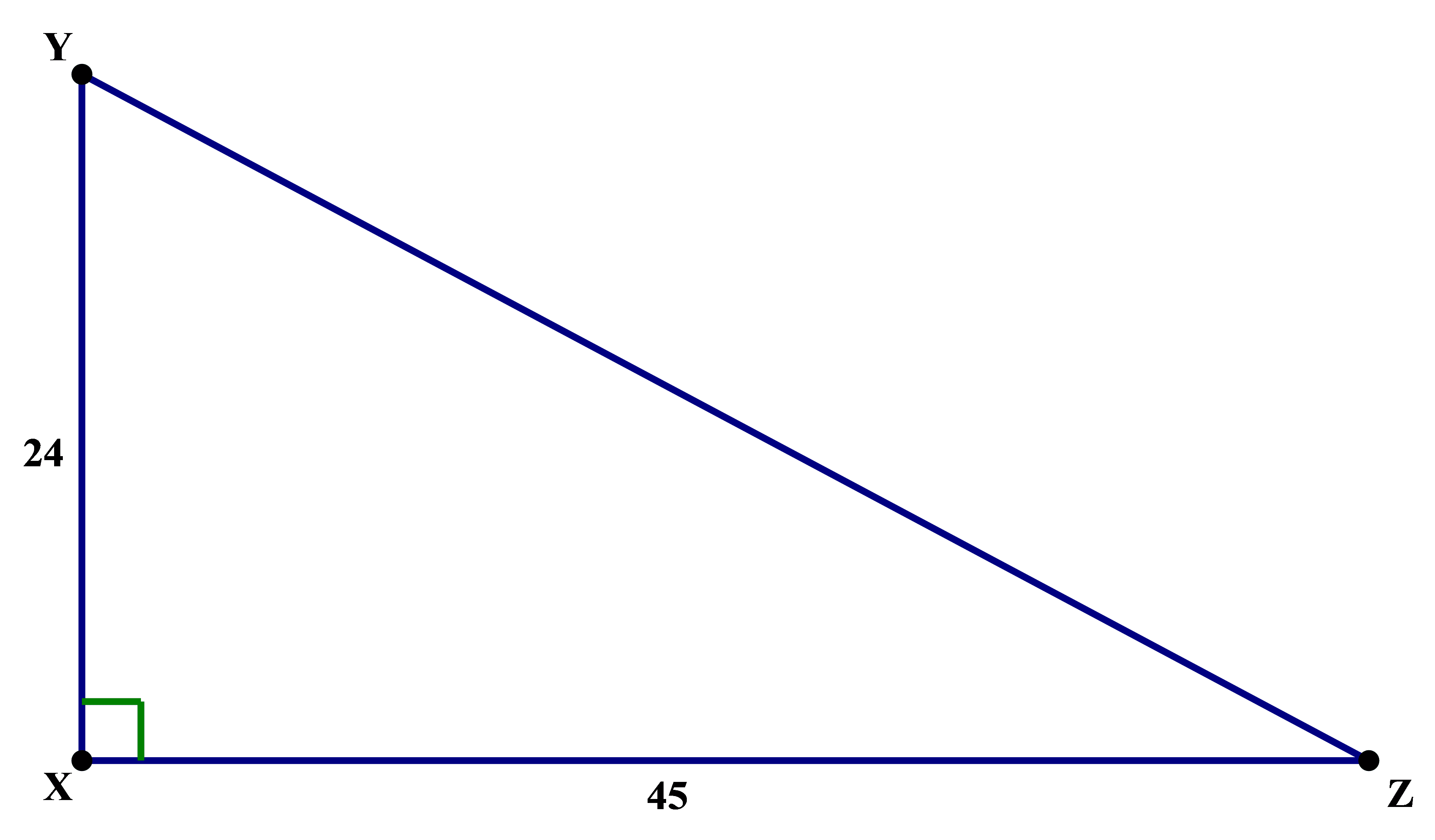
Imagine on the GMAT, you see this:
That’s the diagram, and you are asked to find the length of YZ — you are given five answer choices, any of which looks like it could be plausible at first blush. Well, the unskilled GMAT taker will consume a great deal of time squaring 24, then squaring 45, then adding those together and — Gadzooks! — trying to figure out the square root of the four-digit number that results. 🙁 It’s MUCH easier simply to recognize that 24 = 3*8 and 45 = 3*15, so we are clearly dealing with 3 times the (8, 15, 17) triplet, which we conveniently have memorized. That means the answer must be YZ = 3*17 = 51. 🙂
Armed with these tricks, take another look at the practice problems again, before reading the explanations below. Also, here’s a Magoosh practice GMAT question that uses one of these Pythagorean triplets:
4) http://gmat.magoosh.com/questions/100
Practice question explanations
1) Clearly, the wrong approach would be to square 48 and 60, subtract, and without calculator try to take the square root of the resultant four-digit number. Not fun! A little GCF exploration reveals: 48 and 60 have a GCF = 12. More to the point, 48 = 4*12, and 60 = 5*12, so clearly we have the (3, 4, 5) triplet multiplied by 12. That means the missing side must be AC = 3*12 = 36. Answer = B
2) For those who would like the visual, here’s a diagram:
The purple line is the actual distance we want to find. One very important trick to know: when you need to find a diagonal distance in the x-y plane, always use the Pythagorean Theorem. We draw the connecting horizontal and vertical lines, shown in green here, to create a right triangle, the hypotenuse of which is the distance we want. Horizontal & vertical distances are very easy in the x-y plane: we simply count, or subtract the corresponding coordinates. These x- and y-distances are:
These are the lengths of the two green lines. Lo and behold: our old friend, the (8, 15, 17) triplet! Without any further calculations, we see immediately that the distance between these two points must be 17 units. Answer =
3) We will subdivide the figure as shown.
Notice, we constructed KR, such that KR is perpendicular to MN. This makes KLMR a rectangle and KRN a right triangle. S is the midpoint of KN, so that JS is the median & altitude of isosceles triangle JKN. (Since it’s easy to find the area of rectangles and right triangles, those make particularly good choices for subdivision units when you have to find area.)
Now, we will figure things out piece-by-piece. First of all, a particularly easy piece is rectangle KLMR: Area = bh = 4*8 = 32.
The problem gives that MN = 10, and we know MR = 4, so NR must equal 6, and KR must equal 8. These are two legs of the Pythagorean triplet (6, 8, 10), which is the (3, 4, 5) triplet times two. This means we know KN = 10. We also know the area of triangle KRN is: Area = 0.5*bh = 0.5*6*8 = 24.
Since we know KN = 10, we know the midpoint divides that in half, so KS = SN = 5. Notice, we now have two right triangles, KJS and NJS, each with a leg of 5 and a hypotenuse of 13. This is another one of the triplets, (5, 12, 13)! Immediately, without further calculation, we know JS = 12. Now we can find the area of the big isosceles triangle JKN: Area = 0.5*bh = 0.5*12*10 = 60.
Total area = (area of rect. KLMR) + (area of triangle KRN) + (area of triangle JKN)
= 32 + 24 + 60 = 116
Answer = E


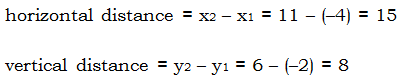




Leave a Reply