What are the most essential topics of algebra that you need to know to succeed in GMAT math? How many formulas and equations do you have to memorize? Why must we be tortured by all this math???
The good news is that it doesn’t take a huge amount of time or energy to master the basics. Most likely, you already have the fundamentals down.
![]() Of course, it never hurts to review, so you might want to check out these first: Introduction to Algebra and FOIL on the GMAT: Simplifying and Expanding.
Of course, it never hurts to review, so you might want to check out these first: Introduction to Algebra and FOIL on the GMAT: Simplifying and Expanding.
This post is intended to help you gain the edge if you already have a solid foundation. By recognizing and taking advantage of some common algebraic expressions or patterns, and by remembering rather than memorizing (GMAT Math: Memory vs. Memorizing), you can substantially improve your ability to obtain the correct answer on even the most challenging algebra questions on the GMAT!
Table of Contents
Three Essential Formulas for GMAT Algebra

Here are two algebraic equations and one formula that you should remember for the GMAT Quant section.
- Difference of Two Squares: \(a^2 – b^2 = (a-b)(a+b) \)
- Squaring a Binomial: \((a \pm b)^2 = a^2 \pm 2ab + b^2 \)
- The Discriminant: \(D = b^2 – 4ac \)
There is a common theme among the three items. In one way or another, they all have something to do with quadratic expressions. These tend to be more difficult to work with than linear equations, simply because the tools look more complicated.
Using the Patterns
The first two items in the list pertain to factoring—you can check out this post for more on that topic: Algebra on the GMAT: How to Factor.
The idea is that you can replace the expression on the left of the equals sign by the one on the right, and vice versa. This technique is often used in simplifying algebraic expressions. The practice problems below will also help you to understand when to use this strategy. The third item, the discriminant, is a powerful tool to help analyze the roots of quadratic equations without ever having to find the roots explicitly.
![]() To see these concepts in action, check out our lesson videos on Factoring – Rational Expressions and Quadratic Equations.
To see these concepts in action, check out our lesson videos on Factoring – Rational Expressions and Quadratic Equations.
GMAT Algebra Practice Problems
Now let’s see if we can spot and use those three patterns in the two types of questions on GMAT Quant!
Problem Solving Questions
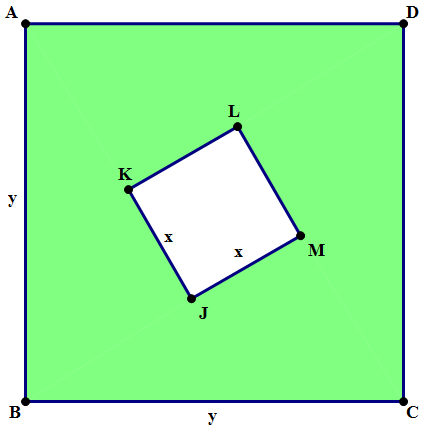
- ABCD is a square with a side \(y \), and JKLM is a square with side \(x \). If Rectangle S (not shown) with length \(x + y \) has the same area as the shaded region above, what is the width of Rectangle S?
First of all, notice that the shaded area, quite literally and visually, is the difference of two squares — Area \(= y^2 – x^2 \). We know from the Difference of Two Squares pattern, this factors into: Area of ABCD \(= y^2 – x^2 = (y + x)(y – x) \) Rectangle S is supposed to have the same area, and it has a length of \(y + x \), which is one of the factors in the above expression. Therefore, the other factor \(y – x \) must be the width of Rectangle S.
Click here for the answer
C.
- What is the largest integral value of \(m \) such that the quadratic equation \(x^2 – 10x + m \) will have two unique solutions?
Click here for the answer
B.
This question is made for the discriminant! You won’t have to guess and check if you know how to use the formula appropriately. To find \(D \), plug in the following to the formula:
\(a = 1 \)
\(b = -10 \)
\(c = m \)
\(D =\) \(b^2\)\( – 4\)\(a\)\(c\)
\(D =\) \((-10)^2\) \(- 4\)\((1)\)\((m)\) \(= 100 – 4m \)
Now, we know that we’re looking for two real solutions, so we want \(D = 100 – 4m > 0 \).
\(100 – 4m > 0 \implies 100 > 4m \implies 25 > m \)
So, we get \(m < 25 \). Be careful NOT to choose 25 as your answer! The largest integer that is less than 25 would be 24.
Data Sufficiency Questions
(For instructions and tips, see GMAT Data Sufficiency Tips.)
- The numbers \(a \), \(b \), and \(c \) are all positive. If \(b^2 + c^2 = 117 \), then what is the value of \(a^2 + c^2 \)?
(1): \(a – b = 3 \)
(2): \(\frac{a + b}{a – b} = 7 \)
Click here for the answer
C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
Let \(X = a^2 + c^2 \), the value we are seeking. Now notice that if we subtract the first equation in the prompt from this equation, we get \(a^2 – b^2 = X – 117 \). Thus if we could find the value of \(a^2 – b^2 \), then we could find the value of \(X \).
Statement (1): \(a – b = 3 \)
From this statement alone, we cannot calculate \(a^2 – b^2 \), so we can’t find the value of \(X \). Statement (1), alone and by itself, is insufficient.
Statement (2): \(\frac{a + b}{a – b} = 7 \)
From this statement alone, we cannot calculate \(a^2 – b^2 \), so we can’t find the value of \(X \). Statement (2), alone and by itself, is insufficient.
Statements (1) & (2) combined: Now, if we know both statements are true, then we could multiply these two equations, which cancels the denominator and results in the simple equation \(a + b = 21 \). Then we would have the numerical value of both \(a – b \) and \(a + b \).
Next we can figure out \(a^2 – b^2 \) using the Difference of Two Squares formula: \(a^2 – b^2 = (a-b)(a+b) \).
Finally, we can calculate \(X \) and answer the prompt. Combined, the two statements are sufficient.
- Given that \(P + 2Q \) is a positive number, what is the value of \(P + 2Q \)?
(1): \(Q = 2 \)
(2): \(P^2 + 4PQ + 4Q^2 = 28 \)
Click here for the answer
B. Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
The prompt tells us that \(P + 2Q \) is a positive number, and we want to know the value of \(P \).
Statement (1): \(Q = 2 \)
Obviously, by itself this tells us zilch about \(P \). Alone and by itself, this statement is completely insufficient.
Statement (2): \(P^2 + 4PQ + 4Q^2 = 28 \)
Now, this may be a pattern-recognition stretch for some folks, but this is simply the Squaring a Binomial pattern. It may be clearer if we re-write it like this:
\(P^2 + 2(P)(2Q) + (2Q)^2 = 28 \)
Just think of \(P\) in the role of \(a\) and \(2Q\) in the role of \(b\). Now, applying the pattern, we get:
\(a^2\) \( + 2\) \(a\)\(b\) \( + \) \(b^2\) \( = (\)\(a\)\( + \)\(b\)\()^2\)
\(P^2\)\( + 2\)\((P)\)\((2Q)\)\( + \)\((2Q)^2\)\( = (\)\(P\)\( +\)\( 2Q\)\()^2 = 28\)
With \((P + 2Q)^2 = 28 \), all we have to do is take a square root. Normally, we would have to consider both the positive and the negative square root, but since the prompt guarantees that \(P + 2Q \) is a positive number, we need only consider the positive root, \(P + 2Q = \sqrt{28} \).
This statement allows us to determine the unique value of \(P + 2Q \), so statement (2), alone and by itself, is sufficient.
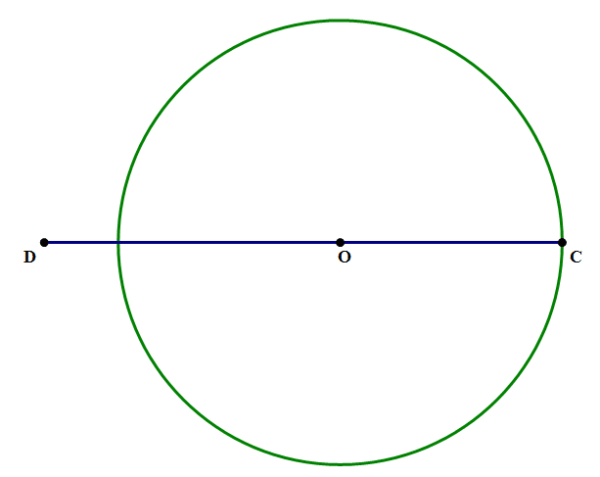
- In the diagram above, O is the center of the circle, DC \(= a \) and DO \(= b \). What is the area of the circle?
(1): \(a^2 – 2ab + b^2 = 36 \)
(2): \(a + b = 22\)
Click here for the answer
A. Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
To find the area of the circle, we need to use Archimedes’ formula, \(A = \pi r^2 \). For that we need the radius, OC, which is not given directly. However, notice that OC = DC – OD, or in other words, \(r = a – b \).
Statement (1): \(a^2 – 2ab + b^2 = 36 \)
A major pattern-matching hit! This is the Squaring a Binomial pattern: \((a – b)^2 = a^2 – 2ab + b^2 \)
\(a^2 – 2ab + b^2 = (a – b)^2 = r^2= 36 \)
In fact, this statement already gives us r^2, so we just have to multiply by \(\pi \) and we have the area. This statement, alone and by itself, is sufficient.
Statement (2): \(a + b = 22 \)
We need \(a – b \), and this statement gives us a value of \(a + b \). If we had more information, perhaps we could use this in combination with other information to find what we want, but since this is all we have, this statement, alone and by itself, is insufficient.
Final Thoughts
GMAT algebra questions do not have to be intimidating. Linear and quadratic expressions and their close relatives make up the bulk of the material that you need to know. By mastering the three essential formulas mentioned above, you will be well on your way to Complete GMAT Domination! (A little too dramatic?)





Leave a Reply