You may remember this GMAT algebra formula, one of the sleekest factoring tricks around:
\(y^2 – x^2 = (y + x)(y – x)\)
This formula, called “the difference of two squares” formula, is a favorite of standardized test writers. A simple enough pattern: see if you can detect where it shows up in the following challenging problems.
1) \(\frac{1}{(2-\sqrt{3})}\)
(A) \(2 – \sqrt{3}\)
(B) \(2 + \sqrt{3} \)
(C) \(1/7\)
(D) \(\frac{\frac{1}{2} – 1}{\sqrt{3}}\)
(E) \(\frac{\frac{1}{2} + 1}{\sqrt{3}}\)
2) What is the sum of a and b?
(1)\( a = 4\)
(2)\(\frac{b^2 – a^2}{ b – a} = 7\)
-
(A) Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
(B) Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
(C) Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
(D) Each statement alone is sufficient to answer the question.
(E) Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
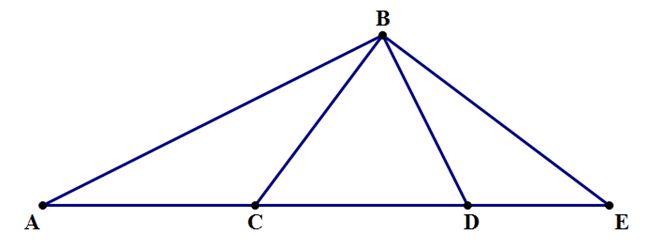
3) In the diagram above, ∠A = ∠ABC, ∠CBD = ∠BDC, and ∠CBE =90°. If AE = 16 and DE = 4, what is the length of BE?
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11
Practice Problem Solutions
1) This involves a relatively sophisticated trick known as “multiplying by the conjugate.” When we have an expression of the form a+\sqrt(b), the “conjugate” of this is a-\sqrt(b). When we multiply a radical expression by its conjugate, we employ the difference of two squares. For example:
\(\frac{1}{(2-\sqrt{3})} = \frac{1}{(2-\sqrt{3})} times \frac{(2 + \sqrt{3})}{(2 + \sqrt{3})} = \frac{(2 + \sqrt{3})}{(2^2 – (\sqrt{3})^2)} = \frac{(2 + \sqrt{3})}{(4 – 3)} = \frac{(2 + \sqrt{3})}{1} = 2 + \sqrt{3}\)
This is answer B. BTW, the trick of multiplying by the conjugate is at the very outside edge of what you might be expected to do the hardest GMAT math problems.
2) The prompt of this DS problem is straightforward.
Statement #1 tells us a = 4, but we have no idea of b, so, by itself, this is not sufficient for finding the sum.
Statement #2 gives us a value for an algebraic expression that lends itself nicely to simplification.
\(7 = {b^2 – a^2}/{b – a} = {(b-a)(b+a)}/{b-a} = a + b\)
Thus, the sum is 7. Statement #2, by itself is sufficient. Answer = B.
3) This is a tricky one. Remember, it’s a diagram drawn to scale, so if all else fails, you can estimate (see this post). But, let’s solve this with math. The fact that ∠A = ∠ABC tells us triangle ABC is isosceles, with AC = BC. The fact that ∠CBD = ∠BDC tells us triangle BCD is isosceles, with BC = CD. The fact that ∠CBE = 90° means that (BC)2 + (BE)2 = (CE)2. This means
\((BE)^2 = (CE)^2 – (BC)^2\)
\({} = (CE + BC)(CE – BC)\)
\({} = (CE + AC)(CE – CD)\) (substitutions from the two isosceles triangles)
\({} = (AE)(DE)\)
\({} = (16)(4) = 64 right BE = 8\)
Answer = B
Here’s a further practice question.