How can you apply the FOIL concept to simplifying and expanding? To get you ready for today’s topic, try working through this GMAT algebra question first:
1) \((2x – 1)*(x + 3) =\)
-
(A) \(x^2 + 3x – 3\)
(B) \(2x^2 + 4x – 3\)
(C) \(2x^2 – 2x – 3\)
(D) \(2x^2 + 3x + 3\)
(E) \(2x^2 + 5x – 3\)
If you find this problem relatively easy, probably most of this post will be for you as well. If this problem makes your head spin, you have found exactly the post you need.
Monomials and Binomials
First, a review of terms. In algebra, any product of numbers and variables is called a “monomial” or a “term.” For example, 2x, \(5y^2\), and \(-3xy/z^2\) are all terms. When we add terms together, we get a polynomial. A polynomial with two terms is a binomial. For example, \((x + 5)\), \((y^5 – x)\), and \((a^2 + b^2)\) are all binomials. A polynomial with three terms is a trinomial. In the question above, each of the five answer choices is a trinomial.
FOIL
The FOIL process is used quite specifically to organize the multiplication of two binomials. The word FOIL is an acronym, which stands for: First, Outer, Inner, Last. Those four words tell you which terms of the binomial to multiply together. Suppose we want to multiply \((3x + 5)*(2x – 7)\). Here is a step-by-step guide to the FOIL process for this.
Those purple terms at the end are the individual FOIL terms — we add those together to get the product:
\((3x + 5)*(2x – 7) = 6x^2 – 21x + 10x – 35 = 6x^2 – 11x – 35\)
That last expression results from combining the two like terms (–21x and 10x) into a single term. That is the process of FOILing. If the question at the beginning of this article was intimidating at first, give it another try now. Here’s a free Magoosh question for practice.
2) http://gmat.magoosh.com/questions/137
Practice question explanation
1) \((2x – 1)*(x + 3) =\) ??
FIRST = \(2x^2\)
OUTER = 6x
INNER = –x
LAST = –3
\((2x – 1)*(x + 3) = 2x^2 + 6x – x – 3 = 2x^2 + 5x – 3\)
Answer = E

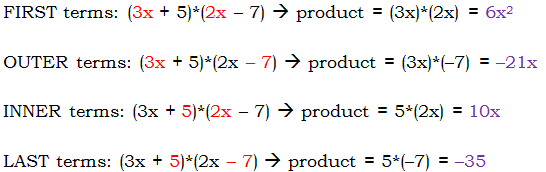




Leave a Reply