First, here are eight practice problems exploring typical percent word problems on the GMAT.
1. The original price of a suit is $200. The price increased 30%, and after this increase, the store published a 30% off coupon for a one-day sale. Given that the consumers who used the coupon on sale day were getting 30% off the increased price, how much did these consumers pay for the suit?
-
(A) $182
(B) $191
(C) $200
(D) $209
(E) $219
2. The profits of QRS company rose 10% from March to April, then dropped 20% from April to May, then rose 50% from May to June. What was the percent increase for the whole quarter, from March to June?
-
(A) 15%
(B) 32%
(C) 40%
(D) 62%
(E) 80%
3. Bert and Rebecca were looking at the price of a condominium. The price of the condominium was 80% more than Bert had in savings, and separately, the same price was also 20% more than Rebecca had in savings. What is the ratio of what Bert has in savings to what Rebecca has in savings.
-
(A) 1:4
(B) 4:1
(C) 2:3
(D) 3:2
(E) 3:4
4. Company KW is being sold, and both Company A and Company B were considering the purchase. The price of Company KW is 50% more than Company A has in assets, and this same price is also 100% more than Company B has in assets. If Companies A and B were to merge and combine their assets, the price of Company KW would be approximately what percent of these combined assets?
-
(A) 66%
(B) 75%
(C) 86%
(D) 116%
(E) 150%
5. There are 300 seniors at Morse High School, and 40% of them have cars. Of the remaining grades (freshmen, sophomores, and juniors), only 10% of them have cars. If 15% of all the students at Morse have cars, how many students are in those other three lower grades?
-
(A) 600
(B) 900
(C) 1200
(D) 1350
(E) 1500
6. A scientific research study examined a large number of young foxes, that is, foxes between 1 year and 2 years old. The study found that 80% of the young foxes caught a rabbit at least once, and 60% caught a songbird at least once If 10% of the young foxes never caught either a rabbit or a songbird, then what percentage of young foxes were successful in catching at least one rabbit and at least one songbird?
-
(A) 40%
(B) 50%
(C) 60%
(D) 80%
(E) 90%
7. A book store bought copies of a new book by a popular author, in anticipation of robust sales. The store bought 400 copies from their supplier, each copy at wholesale price W. The store sold the first 150 copies in the first week at 80% more than W, and then over the next month, sold a 100 more at 20% more than W. Finally, to clear shelf space, the store sold the remaining copies to a bargain retailer at 40% less than W. What was the bookstore’s net percent profit or loss on the entire lot of 400 books?
-
(A) 30% loss
(B) 10% loss
(C) 10% profit
(D) 20% profit
(E) 60% profit
8. At a certain symphonic concert, tickets for the orchestra level were $50 and tickets for the balcony level were $30. These two ticket types were the only source of revenue for this concert. If R% of the revenue for the concert was from the sale of balcony tickets, and B% of the tickets sold were balcony tickets, then which of the following expresses B in terms of R?
Solutions will be given at the end of this article.
Thoughts on percents
First of all, here are some previous blogs on percents:
(1) Fundamentals of percents, including using multipliers for percent increase and decreases.
(2) Solution of a percent with variables problem, from the OG
(3) Another solution of percent with variables problem, from the OG
(4) Scale factors & percent change
(5) Solution & Mixing problems
Especially in those first three, you can find some useful hints for the foregoing problems.
The BIG percent mistake
Folks who are rusty at math and/or returning to it after a long absence may not appreciate something known well to anyone who writes math problems: certain mistakes are as predictable as clockwork. Anyone who writes problems knows — in such-and-such kind of problem, the vast majority of test-takers will make such-and-such very predictable mistake. Of course, on any multiple choice standardized test, that predictable mistake consistently will be among the answer choices: it’s as if the test-maker sets up a huge butterfly net, and the unwitting test-takers run into this trap like lemmings running to the sea. I know this sound cruel, but the purpose of a good standardized test question is to distinguish those who know their stuff from those who don’t, and highly predictable errors are great ways to draw such a distinction very clearly.
Obviously, as a test-taker, it is very much to your advantage to learn to spot these very predicable mistake patterns. Just avoiding these will put you well ahead of the pack. In many different articles on this blog, I discuss these predictable mistakes.
The big predictable mistake with percents has a few variations on the same pattern.
(a) if something increases by P%, then decreases by Q%, the net change is not (P – Q)%
(b) if something increases by P%, then increases by Q%, that’s not an increase of (P + Q)%
(c) [special case] if something increase by P%, then decrease by P%, we do not return to the original value.
(d) [more general case] if something increase by P%, then decreases by Q%, then increase by R%, the total change in percent is not (P – Q + R)%
What all of these have in common is a deep root error — you cannot figure out the total percent change of a series of individual percent changes by adding or subtracting the individual percents. That’s the mistake. People see “start at $100, 40% increase, followed by a 40% decrease“, and scores upon score of people, as predictably as the sunrise, will believe and insist without a shadow of a doubt that the end result must be $100. This large crowd will be in unison and they will be wrong.
What’s the correct thing to do? The correct way to treat any series of percent changes is to express each change as a multiplier, and then multiply all the multipliers. That first blog above talks about creating the multipliers for percent increases & decreases. Once we have that, we can figure out the real change. For example, the multiplier for a 40% increase would be: 1 + 0.40 = 1.4, and the multiplier for a 40% decrease would be 1 – 0.40 = 0.6; now, 1.4*0.6 = = 0.84, so the final price in fact would be $84, which is a 16% decrease.
Summary
If the foregoing discussion gave you any insights, you may want to re-read the practice problems before reading the solution. Here’s another practice problem from the Magoosh Product:
9. http://gmat.magoosh.com/questions/2584
If you have any observations or questions, please let us know in the comments section.
Practice problem explanations
1) Given the foregoing discussion, it may be obvious now the trap-mistake answer is (C). Even if you can’t remember the correct thing to do, at the very least, learn to spot the trap!
The multiplier for a 30% increases is 1 + 0.30 = 1.3, and the multiplier for a 30% decrease is 1 – 0.30 = 0.70, so the combined change is 1.3*0.7 = 0.91, 91% percent of the original, or a 9% decreases. Now, multiply $200*0.91 = $182. Answer = (A).
2) Given the foregoing discussion, it may be obvious now the trap-mistake answer is (C), which results from simply adding and subtracting the percents. We need multipliers.
multiplier for a 10% increases = 1 + 0.10 = 1.1
multiplier for a 20% decreases = 1 – 0.20 = 0.8
multiplier for a 50% increases = 1 + 0.50 = 1.5
Now, multiply these. First, multiply (0.8) and (1.5), using the doubling & halving trick. Half of 0.80 is 0.40, and twice 1.5 is 3
(0.8)*(1.5) = (0.4)*(3) = 1.2
Now, multiply this by 1.1
1.2*1.1 = 1.32
Thus, the three percent changes combined produce a 32% increase. Answer = (B).
3) The trap answer here would be to take the ratio of 80% and 20% — those don’t represent actually amounts that other person has, just the differences between amounts owned and the cost of the condo. Think of this in terms of multipliers. Use the variables:
B = amount Bert has in savings
R = amount Rebecca has in savings
P = price of the condominium
Then in terms of multipliers, the information given tells us that P = 1.8*B, and P = 1.2*R. Set these equal.
1.8*B = 1.2*R
Answer = (C)
4) There are a few ways to solve this. This is plug-in approach. Suppose Company A has $100 in assets. (Yes, unrealistic, but a convenient choice.) Then Company KW is being sold for 50% more = $150. Now, this $150 is 100% more than what company B has in assets —- i.e., $150 is double what company B has in assets, so company B has $75 in assets. Now, suppose companies A & B pool their resources — together, they have $175 in assets.
Notice, first of all, combined they have more in assets than the cost of KW, the price of KW would be a percent less than 100%. Even if nothing else, we could eliminate (D) & (E), and practice solution behavior.
Part = price of KW = $150
Whole = combined assets = $175
Answer = (C)
5) Let x = the number of students other than seniors (freshmen + sophomores + junior). We know 40% of the 300 seniors have cars. Well, 10% of 300 is 30, so 40% is 4 times this —- 4*30 = 120 seniors have cars. We know 10% of the other students have cars, so that would be 0.1*x. The total number of students with cars is 120 + 0.1x. That’s the PART.
The total number of students = 300 + x. That’s the WHOLE.
PART/ WHOLE x 100% = 15%, which means that PART/ WHOLE = 0.15, which means PART = 0.15*(WHOLE). That can be our equation.
(120 + 0.1x) = 0.15(300 + x)
120 + 0.1x = 45 + 0.15x
75 + 0.1x = 0.15x
75 = 0.15x – 0.10x = 0.05x
150 = 0.10x
1500 = x
Answer = (E)
6) This is less about percents and more about probability, particularly the probability OR-rule. Let R = the event that a young fox catches at least one rabbit, and let S = the event that a young fox catches at least one songbird. Using algebraic probability notation, we know P(R) = 0.8 and P(S) = 0.6. We know P((not R) and (not S)) = 0.1, and the complement of [(not R) and (not S)] would be [R or S], so by the complement rule, P(R or S) = 1 – 0.1 = 0.9. The question is asking for P(R and S). The OR rule tells us
P(R or S) = P(R) + P(S) – P(R and S)
0.9 = 0.6 + 0.8 – P(R and S)
0.9 = 1.4 – P(R and S)
0.9 + P(R and S) = 1.4
P(R and S) = 0.5
Answer = (B)
7) First of all, amount paid = 400*W. That was the bookstore’s total expenditures. The total revenue came in three stages
150 copies @ 80% more than W = 150*1.8W = 300*.9W = 270W
100 copies @ 20% more than W = 100*1.2W = 120W
150 copies @ 40% less than W = 150*0.6W = 300*0.3W = 90W
Notice, all the percent changes were converted to multipliers. Also, notice the use of the doubling & halving trick in the first and third lines.
Total revenue = 270W + 120W + 90W = 480W
Well, the store took in more revenue than they spent, so they made a profit, not a loss. Notice that 10% more than 400 would be 440, so 480 would be a 20% increase.
Answer = (D)
8) There are a few different methods of solution. I will show a numerical approach. Let’s try some simple cases — suppose they sold nothing but balcony tickets: then B = 100 and R = 100. If we plug in R = 100 …
Right away, with one choice, we know that (A) and (C) are out. At this point, even if we could do nothing else, we could still use solution behavior.
Now, suppose the revenue they took in was half and half, so that R = 50%. Well, the prices of balcony to orchestra tickets are in a ratio of 3:5, so in order for the revenue from balcony tickets to equal the revenue from orchestra tickets, they would have to be sold in the reciprocal ratio of 5:3 (if you think about it, this just uses the fact that A*B = B*A). This means that 5/8 of the tickets sold would be balcony tickets. (For this logic, see the Ratio blog for information on portioning.) Thus, if we plug in R = 50, we should get B = (5/8)*100 — notice, we don’t actually need to calculate that out: the fraction is fine. In the calculations below, notice the use of the doubling & halving trick in the denominator, to get the factor of 100.
Backsolving gets us to answer (D) very efficient.
Now, here’s an algebraic approach, which is longer, but some folks want to see this anyway for the algebra practice:
Let N = the total number of tickets sold. Then:
Therefore,
In the big fraction, in each term: cancel the N’s, cancel a factor of 10, and cancel the “divided by 100”:
Multiply both sides by the denominator.
R*(500 – 2B) = (3B)*100
500R – 2RB = 300B
Get all the B’s on one side
500R = 2RB + 300B
B*(2R + 300) = 500R
Answer = (D)
That’s the full-blown algebraic solution, although why anyone would want to slog through all that instead of using backsolving is beyond me!!

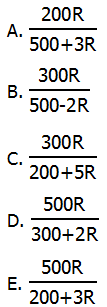

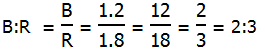
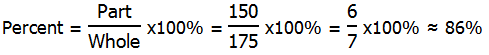
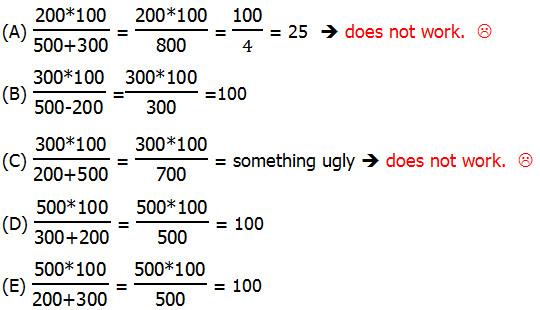
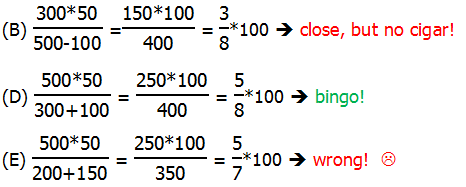
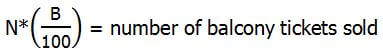

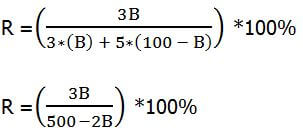
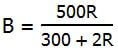



Leave a Reply