This is, among other things, a case study of one of the harder Data Sufficiency problems in the OG.
Percents as Multipliers
You can find several good tips on percent problems at this post. The most relevant here is the idea of a percent as multiplier. To change a percent into a multiplier:
(a) change it from a percent to a decimal
(b) for a percent increase, keep it positive; for a percent decrease, make it negative.
(c) add that to one.
For example, for a 12% decrease,
(a) 12% > 0.12
(b) it’s a decrease, so -0.12
(c) 1 + (-0.12) = 0.88
That final number, 0.88 is the multiplier for a 12% decrease. If we want to decrease any quantity by 12%, all we have to do is multiply by that multiplier.
The DS Problem in the OG
Here’s the problem from the OG, practice DS #120.
120) The annual rent collected by a corporation from a certain building was x percent more in 1998 than in 1997, and y percent less in 1999 than in 1998. Was the annual rent collected by the corporation from the building more in 1999 than in 1997?
1. x > y
2.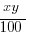 <
<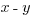
-
(A) Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
(B) Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
(C) Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
(D) Each statement alone is sufficient to answer the question.
(E) Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
The Tempting Wrong Answer
When a percent increase is combined with a percent decrease on the GMAT, the one archetypal mistake the testmakersare trying to educe is idea that you can find the net result by simply adding and subtracting percents. Increase of 20%, followed by a decrease of 15% — the huge mistake to say 20 – 15 = 5%. That’s like a huge booby trap the GMAT sets up every time, and test after test the unsuspecting masses predictably fall into it in swarms. Here, statement #1 is all about that huge mistake. Many people will mistakenly think (1) is sufficient, but it’s not.
When a percent increase is combined with a percent decrease on the GMAT, you need to multiply the multipliers. For example, 20% increase means that the multiplier = 1.20; 15% decrease -> multiplier = 0.85. Combination = 1.20*0.85 = 1.02, a 2% increase.
In particular, increasing by a percent, then decreasing by that same percent, does not leave you in the same place. Consider an increase of 50% followed by a decrease of 50%. Start at $100. Increase by 50% to $150. Now, decrease by 50%, from $150 to 75%. The net result of a 50% increase, followed by a 50% decrease, is a 25% decrease.
Solution
Call the initial 1997 amount of rent A. It increased x% from 1997 to 1998. Notice that x% as a multiplier is (1 + x/100), so the amount of rent in 1998 is:
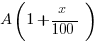
Then, it decreased y% from 1998 to 1999. The multiplier now is 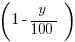 , so the amount of rent in 1999 is:
, so the amount of rent in 1999 is:
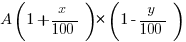
So, in order for the rent to be more in 1999 than in 1997, what multiplies A here, the composite factor multiplying A, must be greater than one.
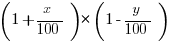 >
> 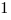
FOIL out the left side:
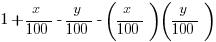 >
> 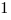
Subtract 1 from both sides:
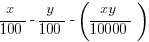 >
> 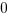
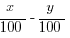 >
> 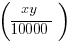
Multiply both side by 100, to clear some of the fractions
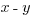 >
> 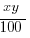
This is the condition for the rent in 1999 being larger than the rent in 1997. Notice this equivalent to Statement #2. Since statement #2 is another form of the statement that the rent in 1999 is larger than the rent in 1997, it is sufficient, and the answer is B.
Here’s a practice PS question exploring some of the same ideas.
http://gmat.magoosh.com/questions/30






Leave a Reply