First, a bank of eight practice problems
1) A certain zoo has mammal and reptiles and birds, and no other animals. The ratio of mammals to reptiles to birds is 11: 8:5. How many birds are in the zoo?
Statement (1): there are twelve more mammals in the zoo than there are reptiles
Statement (2): if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1
2) In a certain large company, the ratio of college graduates with a graduate degree to non-college graduates is 1:8, and ratio of college graduates without a graduate degree to non-college graduates is 2:3. If one picks a random college graduate at this large company, what is the probability this college graduate has a graduate degree?
3) Dan’s car gets 32 miles per gallon. If gas costs $4/gallon, then how many miles can Dan’s car go on $50 of gas?
-
(A) 61.25 miles
(B) 256 miles
(C) 400 miles
(D) 1600 miles
(E) 6400 miles
4) For a certain concert, the price of balcony tickets was exactly half the price of orchestra tickets. The ratio of balcony to orchestra tickets sold was 3:2. What was the price of one orchestra ticket?
Statement (1): the total revenue taken in from tickets of both kinds was $4200
Statement (2): the difference between the number of balcony tickets sold and the number of orchestra tickets sold was 40
5) At a certain high school, there are three sports: baseball, basketball, and football. Some athletes at this school play two of these three, but no athlete plays in all three. At this school, the ratio of (all baseball players) to (all basketball players) to (all football players) is 15:12:8. How many athletes at this school play baseball?
Statement (1): 40 athletes play both baseball and football, and 75 play football only and no other sport
Statement (2): 60 athletes play only baseball and no other sport
6) In a certain class, the ratio of girls to boys is 5:4. How many girls are there?
Statement (1): If four new boys joined the class, the number of boys would increase by 20%.
Statement (2): If the number of girls increases by 50%, then after such an increase, the probability that a randomly chosen student would be a boy would be 8/23
7) If 28 passes to a show cost $420, then at the same rate, how much will 42 passes cost?
-
(A) $500
(B) $560
(C) $630
(D) $700
(E) $840
8) Metropolitan Concert Hall was half full on Tuesday night. How many seats are in the Hall?
Statement (1): If the number of people in the Hall increased by 20% from Tuesday night to Wednesday night, then the Hall would be 60% full on Wednesday night.
Statement (2): If 20 more people showed up on Tuesday night, that would have increased the number of people in the Hall by 4%.
Answers will come at the end of the article.
Ratios and proportions: a review
Probably ratios and proportions have been on your radar since some time in grade school or middle school, when they are introduced. You remember there are a lot of “mathy” facts related to these things, but it’s a bit blurry. Here are a few quick facts as reminders.
1. What is a ratio? Fundamentally, a ratio is a fraction, and is subject to all the laws of fractions. “Ratios” and “fractions” are mathematically identical.
2. What is a proportion? Is it the same as a ratio? No, a proportion is NOT the same as a ratio. Whereas a ratio is single fraction by itself (e.g. 1/3), a proportion is an equation that sets two ratios equal to each other (e.g. 1/3 = 4/12). See the fraction post for a refresher on what you can and can’t cancel in a proportion.
3. When geometric figures are similar, the sides are proportional. Geometric similarity is a topic rife with ratios and proportions. One helpful idea discussed in that post is the idea of a scale factor, which, it turns out, is helpful in many many proportional situations well beyond anything having to do with geometry.
4. Percents and probabilities are specialized cases of ratios, and either gives you very much the same kind of information.
Those are four simple ideas, and there’s one more, but it takes a little setting up to express. Let’s divide the mathematical information that can appear in a problem into two categories. The first category is “ratio information”, and this includes any statements about percents or probability information. The second I’ll call, for lack of a better term, “count information” — not a percent or ratio, but an actual count — i.e. how many people or animals or whatever; it could be how many in any particular group, the sum or difference of multiple groups, or how many are in the whole population. This leads us the final important simple idea:
5. To get count information as an output, you need some count information as an input. If you all you have is ratio information as an input, it is impossible to get count information as an output.
Ratios and portioning
Suppose, in some population, there are three kinds of things, A & B & C, and they are in a proportion of 3:8:4. That’s ratio information. Suppose we want to know either the percent that A makes of the whole, or the ratio of A to the whole. That’s also ratio information, so we should be able to calculate it from that given ratio.
It can be very helpful to understand ratios in terms of “parts”. For every 3 parts of A, there are 8 parts of B and 4 parts of C. To get the whole in the same ratio, we simply add up the parts — 3 + 8 + 4 = 15 parts. Keep in mind, we have zero information about the actual size of the population — we have no count information. This simply indicates the size of the population in the same ratios, so we could say A to the whole is 3/15 = 1/5, and B to the whole is 8/15, and C to the whole is 4/15. This means that A is 1/5 of the whole, or 20%.
Similarly, suppose a class is made up of people with brown eyes and people with blue eyes. 4/7 of the class have brown eyes. Those with brown eyes are four parts, and the whole is seven parts, so those with blue eyes must be the other three parts. Proceeding, we see that those with blue eyes must be 3/7 of the class, the ratio of blue eyes to brown eyes must be 3:4. Thinking about “parts” and portioning can be a powerful way to expand the information you get from any given ratio.
Summary
If you had any realizations while reading this blog, you may want to go back and give the practice problems another glance, before proceeding to the solutions. Here’s another practice question, involving two less-than-lovable baseball teams:
9) http://gmat.magoosh.com/questions/60
If you have any questions about this article, please let us know in the comment section at the bottom!
Practice problem explanations
1) A short way to do this problem. The prompt gives us ratio information. Each statement gives use some kind of count information, so each must be sufficient on its own. From that alone, we can conclude: answer = D. This is all we have to do for Data Sufficiency.
Here are the details, if you would like to see them.
Statement (1): there are twelve more mammals in the zoo than there are reptiles
From the ratio in the prompt, we know mammals are 11 “parts” and reptiles are 8 “parts”, so mammals have three more “parts” than do reptiles. If this difference of three “parts” consists of 12 mammals, that must mean there are four animals in each “part.” We have five bird “parts”, and if each counts as four animals, that’s 5*4 = 20 birds. This statement, alone and by itself, is sufficient.
Statement (2): if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1
Let’s say there are x animals in a “part” — this means there are currently 11x mammals and 5x birds. Suppose we add 16 mammals. Then the ratio of (11x + 16) mammals to 5x birds is 3:1. —-
(11x + 16)/(5x) = 3/1 = 3
11x + 16 = 3*(5x) = 15x
16 = 15x – 11x
16 = 4x
4 = x
So there are four animals in a “part”. The birds have five parts, 5x, so that’s 20 birds. This statement, alone and by itself, is sufficient.
Both statements sufficient. Answer = D.
2) We are given ratio information, and we are asked for ratio information: a probability. That’s fine. For simplicity, let’s use the abbreviations:
P = college graduates with a graduate degree
Q = college graduates without a graduate degree
R = non-college graduates
The two ratios we are given is
P:R = 1:8
Q:R = 2:3
We have combine the ratios, by making the common term the same. The non-college graduates, R, are the common member, accounting for 8 parts in the first ratio, and 3 parts in the second, so we have to multiply the first ratio by 3/3, and the second by 8/8.
P:R = 1:8 = 3:24
Q:R = 2:3 = 16:24
P:Q:R = 3:16:24
Now, the probability about which the question asks is about only college graduates, so ignore the non-college graduates, and just focus on the ratio among college graduates:
P:Q = 3:16
There are 3 + 16 = 19 parts in total, and of those, 3 are the folks in P, so that’s a probability of 3/19. Answer = (D).
3) To get from dollars to gallons, we have to start with the $50, and divide by ($4/gallon) — that cancels the unit of dollars, and leaves us with gallons —– 50/4 gallons. (For the moment, I’ll leave it as that un-simplified fraction).
Now, we need to get from gallons to distance. We multiply by (32 miles/gallon), to cancel the units of gallons, and leave only miles —-
(50/4) gallons*(32 miles/gallon) = (32*50)/4 miles = (8*50) miles = 400 miles
Notice, we didn’t do anything with the four in the denominator until we got a 32 in the numerator with which we could cancel.
Answer = (C)
4) We know the price of a balcony ticket, B = (1/2)*C, or 2B = C, where C = the price of orchestra ticket. The 3:2 ratio tells us that, for some n, the concert sold 3n balcony tickets and 2n orchestra tickets.
Statement (1): the total revenue taken in from tickets of both kinds was $4200
We know total revenue would be (3n) balcony ticket plus (2n) orchestra tickets:
(3n)*B + (2n)*C = (3n)*B + (2n)* 2B = 3nB + 4nB = 7nB = $4200, or nB = 600. The problem with this — we have two variables, n and B. In one extreme case, we could say n = 1 (sold 3 balcony ticket and 2 orchestra tickets), and a balcony ticket cost $600. At another extreme, we could say n = 600 (sold 1800 balcony ticket and 1200 orchestra tickets) and a balcony ticket cost $1. This information alone does allow us to determine a definitive answer to the prompt question. This statement, alone and by itself, is insufficient.
Statement (2): the difference between the number of orchestra tickets sold and the number of balcony tickets sold was 40
Well, balcony tickets are 3 parts, and orchestra tickets are two parts, so there’s one part of difference between them. The statement lets us know: one part = 40, so that allows us to figure out: we sold 3*40 = 120 balcony tickets, and 2*40 = 80 orchestra tickets. That’s great, but unfortunately, with this statement, we get absolutely no financial information, so we can’t solve for a price. This statement, alone and by itself, is insufficient.
Combined statements: now, put this altogether. From the first statement, we got down to the equation nB = 600, and the second statement, in essence, tells us n = 40. Therefore, B = 600/40 = 60/4 = $15. That’s the price of a balcony ticket. The price of an orchestra ticket is twice that, $30. With both pieces of information, we were able to solve for this. Together, the statements are sufficient.
Statement are sufficient together but not individually. Answer = C
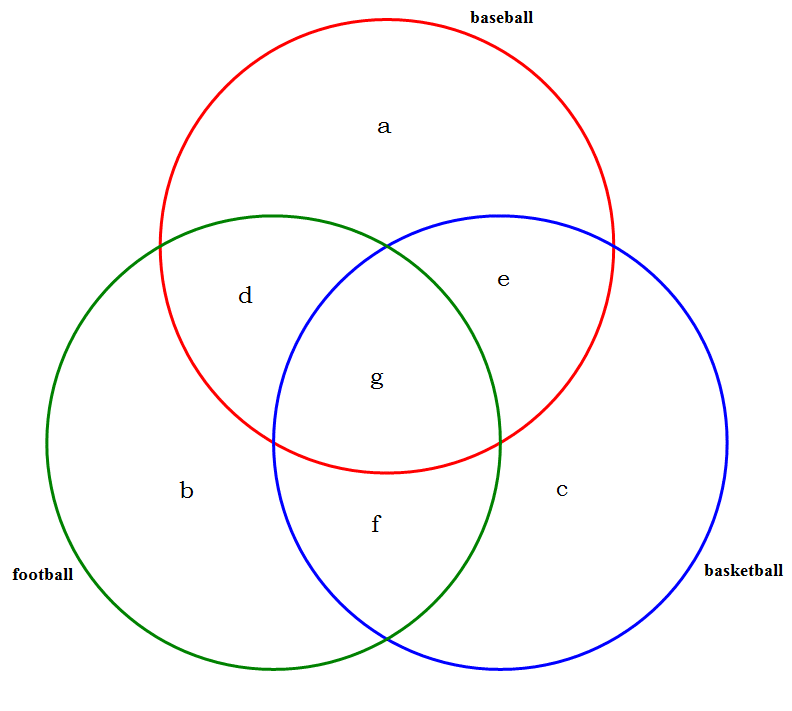
5) This is a tricky one. The ratio 15:12:8 double-counts some students. In terms of a triple Venn diagram:
So, in that diagram
a = folks who play baseball only
b = folks who play football only
c = folks who play basketball only
d = folks who play baseball and football only
e = folks who play baseball and basketball only
f = folks who play football and basketball only
g = folks who play all three sports
We know from the prompt that g = 0, but at the outset, that’s still six unknowns!!
Now, notice:
everyone who plays baseball = a + d + e
everyone who plays basketball = c + e + f
everyone who plays football = b + d + f
So, the ratio given in the problem is:
(a + d + e):(c + e + f):(b + d + f) = 15:12:8
Of course, these are all fractions, so we can’t simplify: there is no way to simplify.
We would like to find the total number of baseball players, a + d + e.
Statement #1 tells us that d = 40 and b = 75. Thus
total number of baseball players = a + 40 + e
We don’t have enough information to calculate this, and we don’t have enough ratio information to solve. This statement, alone and by itself, is insufficient.
Statement #2 tells us a = 60. Thus
total number of baseball players = 60 + d + e
We don’t have enough information to calculate this. This statement, alone and by itself, is insufficient.
Combined statements: Now we know a = 60, b = 75, and d = 40.
total number of baseball players = 60 + 40 + e= 100 + e
total number of football players = 75 + 40 + f = 115 + f
We know the ratio of these two quantities, baseball to football, is 15:8. Unfortunately, that would give us only one equation for two unknowns, e & f. If we can’t solve for these, then we can solve for the total number of baseball players. Even with both statements combined, we cannot determine the answer.
Both statements combined are insufficient. Answer = E
6) Statement (1): If four new boys joined the class, the number of boys would increase by 20%. This means, those four new boys count as 20% of the original boys, which means 2 new boys would be 10% of the original boys, which means there must have been 20 original boys. If we know how many boys, we can use the ratio to calculate how many girls. This statement, alone and by itself, is sufficient.
Statement (2): If the number of girls increases by 50%, then after such an increase, the probability that a randomly chosen student would be a boy would be 8/23. The prompt gives us “ratio information”, and this statement also gives us more “ratio information”. We have absolutely no “count information”, so we can’t figure out the count or number of anything. This statement, alone and by itself, is insufficient.
First statement sufficient, second insufficient. Answer = A
7) We can solve this question by setting up a proportion:
Divide the left fraction, numerator and denominator, by 7:
Now, cancel the factor of 4:
For this multiplication, use the doubling & halving trick — double 15 is 30, and half of 42 is 21:
x = (15)*(42) = 30*21 = $630
Answer = C
8) The prompt gives us “ratio information”.
Statement #1 also gives us “ratio information”, so there is no way we can calculate a count, such as total number of seats in the hall. This statement, alone and by itself, is insufficient.
Statement #2: 20 people would be 4% of the audience. Divide by two — 10 people would have be 2%; now multiply by five — 50 people would have been 10% of the audience; now multiply by ten — 500 people would be 100% of the audience on Tuesday night. Since the concert hall was half full, there must be 1000 seats in total. This piece of information allows us to solve for the answer to the prompt question. This statement, alone and by itself, is sufficient.
First statement insufficient, second sufficient. Answer = B
Special Note:
To find out where ratios and proportions sit in the “big picture” of GMAT Quant, and what other Quant concepts you should study, check out our post entitled:
What Kind of Math is on the GMAT? Breakdown of Quant Concepts by Frequency


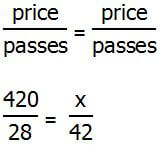
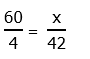
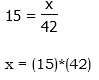




Leave a Reply