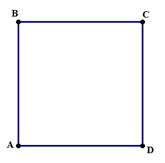
Consider the following geometry Data-Sufficiency Questions. All are related to the diagram below:
1) Is quadrilateral ABCD a square?
(1) AB = CD
(2) A = 90º
- (A) Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
- (B) Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
- (C) Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
- (D) Each statement alone is sufficient to answer the question.
- (E) Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
(Use these answer choices for all of the following questions.)
2) Is quadrilateral ABCD a square?
(1) AB = BC = CD
(2) AB = AD
3) Is quadrilateral ABCD a square?
(1) AB = BC = CD = DA
(2) A = 90º
4) Is quadrilateral ABCD a square?
(1) A = C = 90º
(2) AB = AD
5) Is quadrilateral ABCD a square?
(1) ABCD is a parallelogram
(2) AB = CD
6) Is quadrilateral ABCD a square?
(1) A = B = C = 90º
(2) AB = AD
At the end of the post I will give answers and explanations. I will just say right now: four of these have the answer E, and other two have the answer C. None of these has an answer of A, B, or D. Part of what that means is: no single statement of the twelve above is sufficient by itself. Takeaway: it’s not easy to prove something is a square.
Parallelogram Facts
Fact #1: the rectangle, rhombus, and square are all parallelograms; they are “special cases” within the larger category of parallelograms.
Fact #2: the square is a kind of rectangle: it’s a rectangle with all equal sides.
Fact #3 is the square is a kind of rhombus: it’s a rhombus with four right angles.
Therefore, proving something is a square often entails proving that it a parallelogram, a rectangle, and a rhombus. If it’s possible the shape is not a rectangle, not a rhombus, or not a parallelogram, then it’s not definitive that it is a square.
How do we prove something is a parallelogram? Well, we can use any of what I like to call the BIG FOUR parallelogram properties:
(1) both pairs of opposite sides are parallel
(2) both pairs of opposite sides are congruent
(3) both pairs of opposite angles are congruent
(4) diagonals bisect each other
Any one of those properties is sufficient to prove the other three; any one of them is sufficient to prove a shape is a parallelogram. All of them follow immediately if we know the shape is a parallelogram. Therefore, establishing any of the BIG FOUR can be a step toward proving something is a square.
The Square is Elite
One problem with geometry Data Sufficiency is: there are many things that could be true. In any of the six questions above, the shape could be a square. That, though, is not what GMAT Data Sufficiency is about. GMAT Data Sufficiency is about: what do you know must be true, of mathematical necessity, without a shadow of a doubt?
There are scads of possible quadrilaterals. The square is unique: it is an elite shape among the quadrilaterals, one out of millions.
Think of this analogous DS-like question:
7) Is my next door neighbor the President of the United States?
(1) My next door neighbor has two arms and two legs
(2) My next door neighbor’s last name begins with a vowel
Now, of course, both Statements #1 and #2 would be true if my next door neighbor were the President of the United States, but again, that’s not what DS questions are about. Of course, the answer to this would be E. If you told me statements #1 and #2, and I leaped to the conclusion that your next door neighbor must be the President of the United States, that conclusion would be extremely gullible on my part. It would be gullible because I was leaping to such a specific conclusion while given only very broad and general constraints.
In precisely the same way, the geometry Data Sufficiency questions on the GMAT attempt to catch the test-takers in a similar gullibility.
Having said all this, you may want to go back and reconsider the questions before you look at the answers and explanations below.
Here’s another free DS question on the same topic: http://gmat.magoosh.com/questions/1023
Practice Question Answers and Explanations
(1) E; (2) E;(3) C;(4) E;(5) E;(6) C;
In the diagrams below, asymmetries have been exaggerated for visual clarity.
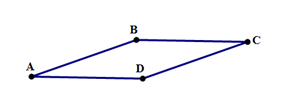
(1) Here’s an irregular quadrilateral that satisfies both statements. Both statements combined don’t determine conclusively that the figure is a square. Answer = E.
(2) The statements combined do determine that all four sides are congruent, which means ABCD must be a rhombus, but we have no information about the angles, so we can’t conclude anything about a square. Answer = E.
3) Statement #1 determines that ABCD is a rhombus, which necessarily implies the BIG FOUR. Statement #2 adds a right angle. A rhombus with a right angle is a square. Answer = C.
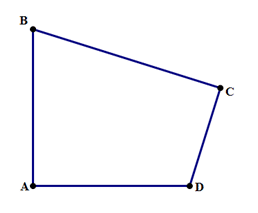
4) Here’s an irregular quadrilateral that satisfies both statements. Both statements combined don’t determine conclusively that the figure is a square. Answer = E.
(5) Statement #1 tell us ABCD is a parallelogram, which immediately implies the BIG FOUR properties. Statement #2 is included already in the on the BIG FOUR, so it adds nothing new. With the combined statements, we only know ABCD is a parallelogram, nothing else for sure. Answer = E
(6) Statement #1 guarantees the shape is a rectangle, which immediately implies the BIG FOUR. Statement #2 adds that two adjacent sides are congruent. A rectangle with adjacent sides congruent is a square. Answer = C.






Leave a Reply