
You might not feel decimals are the most exciting thing in the world, but just look at our friend  , a decimal with its own holiday! In this edition of GMAT Math, we’re going over two specific types of decimals: terminating and repeating decimals. Learn about how to identify and solve questions with these decimals. Don’t forget to test your understanding with the practice questions at the end!
, a decimal with its own holiday! In this edition of GMAT Math, we’re going over two specific types of decimals: terminating and repeating decimals. Learn about how to identify and solve questions with these decimals. Don’t forget to test your understanding with the practice questions at the end!
Rational Numbers
Integers are positive and negative whole numbers, including zero. Here are the integers:
{ … -3, -2, -1, 0, 1, 2, 3, …}
When we take a ratio of two integers, we get a rational number.
- A rational number is any number of the form a/b, where a & b are integers, and b ≠ 0.
- Rational numbers are the set of all fractions made with integer ingredients. Notice that all integers are included in the set of rational numbers, because, for example, 3/1 = 3.
Rational Numbers as Decimals
When we make a decimal out of a fraction, one of two things happens. It either terminates (comes to an end) or repeats (goes on forever in a pattern). Terminating rational numbers include:
1/2 = 0.5
1/8 = 0.125
3/20 = 0.15
9/160 = 0.05625
Repeating rational numbers include:
1/3 = 0.333333333333333333333333333333333333…
1/7 = 0.142857142857142857142857142857142857…
1/11 = 0.090909090909090909090909090909090909…
1/15 = 0.066666666666666666666666666666666666…
When Do Rational Numbers Terminate?
The GMAT won’t give you a complicated fraction like 9/160 and expect you to figure out what its decimal expression is. BUT, the GMAT could give you a fraction like 9/160 and ask whether it terminates or not. How do you know?
Well, first of all, any terminating decimal (like 0.0376) is, essentially, a fraction with a power of ten in the dominator; for example, 0.0376 = 376/10000 = 47/1250. Notice we simplified this fraction, by cancelling a factor of 8 in the numerator. Ten has factors of 2 and 5, so any power of ten will have powers of 2 and powers of 5, and some might be canceled by factors in the numerator , but no other factors will be introduced into the denominator. Thus, if the prime factorization of the denominator of a fraction has only factors of 2 and factors of 5, then it can be written as something over a power of ten, which means its decimal expression will terminate.
- If the prime factorization of the denominator of a fraction has only factors of 2 and factors of 5, the decimal expression terminates. If there is any prime factor in the denominator other than 2 or 5, then the decimal expression repeats.
Here’s some examples of this concept at work:
- 1/24 repeats (there’s a factor of 3)
- 1/25 terminates (just powers of 5)
- 1/28 repeats (there’s a factor of 7)
- 1/32 terminates (just powers of 2)
- 1/40 terminates (just powers of 2 and 5)
Notice, as long as the fraction is in lowest terms, the numerator doesn’t matter at all. Since 1/40 terminates, then 7/40, 13/40, or any other integer over 40 also terminates. Since 1/28 repeats, then 5/28 and 15/28 and 25/28 all repeat; notice, though that 7/28 doesn’t repeat, because of the cancellation: 7/28 = 1/4 = 0.25.
Shortcut Decimals to Know
There are certain decimals that are good to know as shortcuts, both for fraction-to-decimal conversions and for fraction-to-percent conversions. These are:
- 1/2 = 0.5
- 1/3 = 0.33333333333333333333333333…
- 2/3 = 0.66666666666666666666666666…
- 1/4 = 0.25
- 3/4 = 0.75
- 1/5 = 0.2 (and times 2, 3, and 4 for other easy decimals)
- 1/6 = 0.166666666666666666666666666….
- 5/6 = 0.833333333333333333333333333…
- 1/8 = 0.125
- 1/9 = 0.111111111111111111111111111… (and times other digits for other easy decimals)
- 1/11 = 0.09090909090909090909090909… (and times other digits for other easy decimals)
Irrational Numbers
There’s another category of decimals that don’t terminate (they go on forever) and they have no repeating pattern. These numbers, the non-terminating non-repeating decimals, are called the irrational numbers.
- It is impossible to write any irrational number as a ratio of two integers.
Mr. Pythagoras (c. 570 – c. 495 bce) was the first to prove a number irrational: he proved that the square-root of 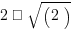 is irrational. We now know: all square-roots of integers that don’t come out evenly are irrational. Another famous irrational number is
is irrational. We now know: all square-roots of integers that don’t come out evenly are irrational. Another famous irrational number is 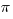 , or pi, the ratio of a circle’s circumference to its diameter. For example,
, or pi, the ratio of a circle’s circumference to its diameter. For example,
That’s the first 70 digits of pi, and the digits never repeat—they go on forever with no repeating pattern. There are infinitely many irrational numbers: in fact, the infinity of irrational numbers is infinitely bigger than the infinity of the rational numbers, but that gets into some math that is much more advanced than what you need to know for the GMAT.
Terminating and Repeating Decimals: Practice Questions
Now here’s your chance to test your understanding! Try to answer these practice questions and then check the answer and explanation.

- 2/27
- 3/2
- 3/4
- 3/8
- 9/16
Show answer and explanation
From our shortcuts, we know 0.166666666666… = 1/6, and 0.444444444444… = 4/9. Therefore (1/6)*(9/4) = 3/8.
Answer = D
And now for a sample question from our GMAT product:
2. Given that
represents a decimal in which the digit k repeats without end, then what is the value of
?
0.1
1
4.5
6
18
Click here for the answer and video explanation!
If you’d like to practice more with decimals, check out our GMAT practice questions with fractions and decimals.


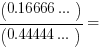
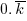 represents a decimal in which the digit k repeats without end, then what is the value of
represents a decimal in which the digit k repeats without end, then what is the value of 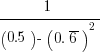 ?
?



Leave a Reply