
Learn the cluster of the most common GMAT math mistakes, mistakes that the exam regularly exploits so you can avoid these pitfalls.
Pattern-Matching,
Good and Bad
The human brain is, far and away, the best pattern-matching machine we have ever seen. No computer comes close. We match patterns for all kinds of things: facial recognition, movies, neighborhood, assessing whether someone is loony, assessing whether someone would make a good friend, etc. Needless to say, because we do so much pattern-matching, our choices are not spot-on correct 100% of the time.
Mathematical Patterns
What’s germane to GMAT Math is that we also learn and understand math via patterns. Like all things in mathematics, what’s mathematically true is absolutely precise, and even a slight change from that may be completely false. That simply does in our pattern-matching right-brain, which likes to fudge to fit things. Hence, there are a some very predictably mathematical patterns that people think are true, or suspect are true, even though they are blatantly false. And, of course, dozens of GMAT Math questions are designed to probe exactly those areas!
Some True Patterns
First of all, let’s talk about two true patterns. True pattern #1 is the Distributive Law, which says that multiplication distributes over addition & subtraction.
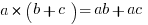
Incidentally, when you go from left to right, the action is called “distributing”, and when you go right to left, the action is called “factoring out.” Those two are a complement pair of actions. Factoring out is a move that is often helpful in solving the more algebraic GMAT problems.
The second doesn’t have a universally recognized name like the first, although it’s sometimes called the “Distributive Law for Exponents,” which says that exponents distribute over multiplication& division.
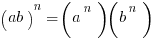
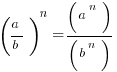
Two special cases of this are square-roots and reciprocals, which are really specific cases of exponents. They both distribute over multiplication.
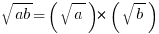
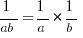
All of these are 100% percent true.
The Not-So-True Patterns
You can almost see where this is going. It’s absolutely true that multiplication distributes over addition and subtraction. It’s absolutely true that exponents (including square-roots and reciprocals) distribute over multiplication and division. BUT, it’s 100% false that exponents, square-roots, or reciprocals distribute over addition and subtraction at any time in any way. The following red equations are examples of false extensions of the pattern.
Take a good look at these. I encourage you to plug in numbers to verify that each one is false. They are close to the correct laws above, but in characteristic mathematical fashion, “close” here means “dead wrong.” Questions that encourage you to make one of these mistakes simply litter the GMAT math sections.
Robust Errors
The pattern-matching function of the brain runs deep, as does our trust in it. Just because you can identify the faulty pattern consciously in a lucid moment doesn’t mean you won’t fall into the same mistake again.
In math pedagogy, these are called “robust errors”: even when you understand clearly why these are false, it’s as if the pattern-matching machinery of the mind draws you back to making the same mistake. If you less than 100% crystal clear about these mistakes, you will make them when you are tired, when you are less focused, and when you are stressed – for example, during the GMAT. I highly recommend that you bookmark this page and reread this article, each time reacquainting yourself with why each mistake is mathematically unsound. I highly recommend you start making a log of the GMAT practice questions that, in some way, solicited one of these mistakes – and whether you fell for it or not.
Taken as a group, these must be the single greatest source of algebra errors on the GMAT. If, through practice, you can learn to catch yourself and prevent yourself from making one of these mistakes every time, this will phenomenally improve your GMAT Quantitative Score.
Dropping the negative sign
Suppose you are solving the equation
5 – 2x = 13
We want to isolate x. One tactic would be to begin by subtracting 5 from both sides. On the right, 13 – 5 = 8. On the left, the 5’s cancel, but with what are we left? It would be a mistake to subtract 5 and wind up with:
I have that in red, with an unequal sign, to emphasize that it is wrong. Of course, the mistake is: when we subtract the 5 and get rid of it, the 2x term does not magically change from negative to positive. It still has a negative sign in front of it. Therefore, the next steps are:
-2x = 8
x = -4
Actually, if you notice any tendency toward making this mistake, I highly recommend: make your first step to add any subtracted variable to other side, to make it positive. If your first step, automatically, is to make the variable positive, then you will be considerably less likely to make this mistake.
Dividing by the numerator
Suppose you have this equation to solve:
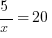
Both sides are clearly divisible by 5, so one possible first step would be to divide by sides by 5. On the right, 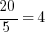 . On the left, the 5’s cancel, but the question is: what is on the left side after dividing by 5? Just x? No! That’s a very tempting mistake to make! In the equation above, x is in the denominator, and “being in the denominator” is not a condition that goes away just because a number in the numerator is cancelled. If we divide by sides by 5, the proper result is
. On the left, the 5’s cancel, but the question is: what is on the left side after dividing by 5? Just x? No! That’s a very tempting mistake to make! In the equation above, x is in the denominator, and “being in the denominator” is not a condition that goes away just because a number in the numerator is cancelled. If we divide by sides by 5, the proper result is
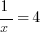
You can multiply by x, and divide by 4 to solve —- or, you simply could take the reciprocal of both sides (always a completely legitimate move when you have fraction = number or fraction = fraction). Either way, the answer is 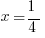 .
.
Distributing a square
These next three mistakes are part of a broad category. First of all, one of most fundamental laws underlying all arithmetic and algebra is a law called the Distributive Law. Symbolically, it states
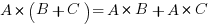
When read left-to-right, it is called distributing: we distribute A over (B + C). When this same equation is read right-to-left, it is called “factoring out.” See this post for a more extended panegyric to the Distributive Law, in a more advanced context. That equation is 100% true, 100% of the time. In words, we can say: multiplication distributes over addition and subtraction. It’s one of the most fundamental laws in all of mathematics.
That pattern is very important, and has a wide variety of applications in elementary and advanced mathematics. For some reason, though, this pregnant pattern is ripe for vast over-generalization. The mind seems almost magnetically drawn to distributing all kind of things other than multiplication over addition and subtraction.
One example is: an exponent. Suppose we are asked to expand algebraically the expression:
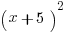
Be careful here, because unless you are a pro at math, your mind is going to be magnetically attracted to the wrong thing to do. Here’s the wrong thing to do:
If you notice, this mistake involves following the Distributive Law pattern, but with an exponent rather than with multiplication. That’s illegal. What’s the correct procedure? Well, squaring anything means multiplying it by itself, so the first step would be:
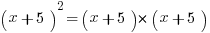
From there, you would FOIL out the expression. That’s the step-by-step way to get to the answer. It can be a very handy shortcut to have the following two patterns memorized.
The Square of a Sum: 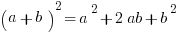
The Square of a Difference: 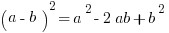
Those formulas take into account the proper FOILing. Memorizing these can be a time-saving shortcut and also might help you to remember to avoid Mistake #3 here.
Distributing a fraction
This is another mistake of the “over-extend the Distributive Law to regions that are not valid” variety. Here is the succinct way to express this mistake.
In other words, you can neither combine nor separate fractions by additions in the denominator. This one has far-reaching ramifications. For example, in the following fraction …
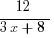
… what can you cancel? NOTHING! If the 12 were over just the 3x, or if the 12 were just over the 8, then you would be able to cancel, but because you can’t separate the fraction, you can do absolutely no canceling. BTW, in the fraction ….
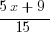
… even though some cancellation is possible, you can’t do any while the fraction is still like this. You have to separate it, by the addition in the numerator (a 100% legitimate move) and then you can cancel:
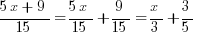
Another related mistake. Suppose we have to solve the following equation.
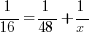
While it’s true in general that you can take the reciprocal of both sides, unfortunately, you can only take the reciprocal of a single number or a single fraction, NOT a sum or difference of fractions.
The reciprocal of a sum is not the sum of the reciprocals. How do you find the reciprocal of a sum? You would have to add the two fractions, using a common denominator, combining them into a single fraction. Here, by far the easiest solution would be to begin by subtracting 1/48 from both sides, and performing the fraction subtraction on the left side, so that you have a single fraction equals 1/x. Then, you would legitimately be allowed to take the reciprocal of both sides to solve.
Distributing a root
The final mistake, yet another example of illegitimately over-extending the pattern of the Distributive Law, is distributing root signs. Succinctly, this mistake says:
You cannot separate a square-root by addition or subtraction. You can separate a root by multiplication or division: see this post for more on that. You can see more about roots in general here.
If you have the equation…
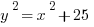
… it is illegal to try to simplify that by taking a square-root of each term:
Think about it. Mr. Pythagoras was a very intelligent individual. If it were possible to simplify 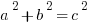 to a + b = c, then that’s how he would have stated the famous theorem. The fact is: he had to state it as
to a + b = c, then that’s how he would have stated the famous theorem. The fact is: he had to state it as 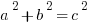 , because it is absolutely illegal to simplify that to a + b = c.
, because it is absolutely illegal to simplify that to a + b = c.
In fact, whereas the former is true for the three side of every right triangle, the latter is not true for the three sides of any triangle. In fact, it constitutes a blatant violation of the Triangle Inequality, a law that is true for every possible triangle.
When you make a mistake during your GMAT preparation—not just on the Quant section—there’s always an opportunity to learn from your errors. Check out the video below for tips, then try out the practice questions!
Practice Questions
1) Find the value of 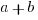
(1) 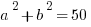
(2) 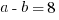
- Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
- Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
- Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
- Each statement alone is sufficient to answer the question.
- Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
2) Is 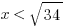 ?
?
(1) 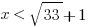
(2) 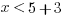
- Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
- Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
- Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
- Each statement alone is sufficient to answer the question.
- Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
Practice Question Answers and Explanations
(1) E; (2) E
In both of those questions, I was bending over backwards trying to lead you into making one of those errors.
1) Clear prompt: find the value of 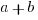 .
.
Statement #1: We cannot take the square root of 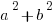 to get
to get 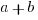 . There’s no way to simplify
. There’s no way to simplify 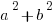 , and the equation
, and the equation 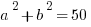 has an infinite number of pairs (a, b) that solve it, each with a different sum. This statement does not allow us to answer the question. Statement #1 is insufficient.
has an infinite number of pairs (a, b) that solve it, each with a different sum. This statement does not allow us to answer the question. Statement #1 is insufficient.
Statement #2: Again, there are an infinite number of pairs (a, b) that satisfy the equation 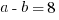 . No conclusion can be drawn about
. No conclusion can be drawn about 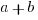 . Statement #2 is insufficient.
. Statement #2 is insufficient.
Statements #1 & #2 Combined: Now, we have two equations for two unknowns, so we can solve.
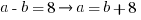
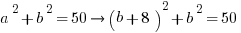
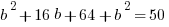
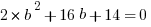
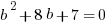
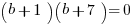
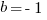
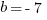
Two solutions: {a = +7, b = -1} or {a = +1, b = -7}.
These two have different sums, so we cannot uniquely determine the value of a + b. Even combined, the statements are insufficient.
Answer = E.
2) The prompt: Is 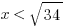 ?
?
Statement #1: We cannot say that 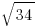 is equal to
is equal to 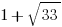 . Like
. Like 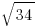 ,
, 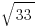 is somewhere between 5 and 6. When we add 1, it’s somewhere between 6 and 7. If we know x is less than a number between 6 and 7, that’s not a guarantee that it’s less than a number between 5 and 6. Statement #1 is insufficient.
is somewhere between 5 and 6. When we add 1, it’s somewhere between 6 and 7. If we know x is less than a number between 6 and 7, that’s not a guarantee that it’s less than a number between 5 and 6. Statement #1 is insufficient.
Statement #2: We cannot say that 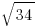 is equal to
is equal to 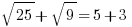 . Knowing that
. Knowing that 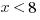 doesn’t tell us conclusively whether or not x is less than
doesn’t tell us conclusively whether or not x is less than 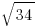 , a number between 5 and 6. Statement #2 is insufficient.
, a number between 5 and 6. Statement #2 is insufficient.
Statements #1 & #2 Combined: Now, the combined conditions just amount to Statement #1, which was more restrictive than Statement #2. We already know that Statement #1 is insufficient, so this means that the combined statements are also insufficient.
Answer = E
For more practice questions, sign up for Magoosh GMAT Prep, which offers hundreds of lessons and practice questions, all with video explanations!

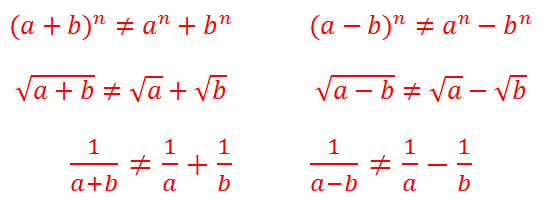

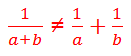
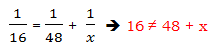




Leave a Reply