Here are ten problems on fractions and decimals, some of which are quite challenging. Remember, no calculator!
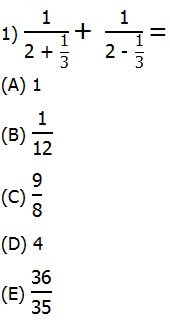
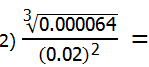
- (A) 0.1
(B) 1
(C) 10
(D) 100
(E) 1000
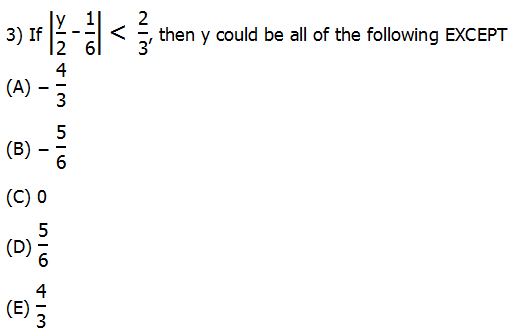
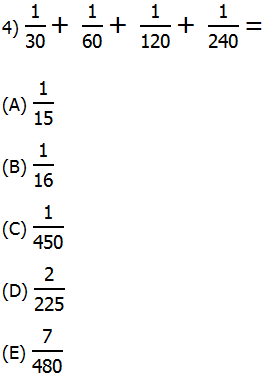
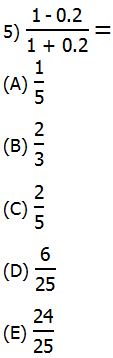
6) Suppose you have access to a large vat of distilled water, several gallons large. You have two precise measuring pipettes, one to measure exactly 1/3 of an ounce and one to measure exactly 1/4 of an ounce. You can pour precisely measured amounts into a beaker, which initially is empty. You can use either pipette to remove distilled water from the vat or from the beaker and use either pipette to dispense water into either of those receptacles, but you cannot use either pipette to take any quantity of distilled water other than the amount for which it is designed. Which of the following represents, in ounces, a precise amount of distilled water you can transfer from the vat to the beaker?
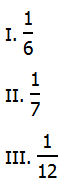
- (A) I only
(B) III only
(C) I and III only
(D) II and III only
(E) I, II, and III
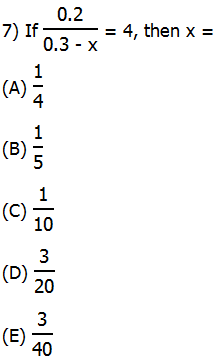
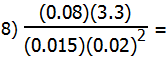
- (A) 440
(B) 6,600
(C) 13,200
(D) 44,000
(C) 132,000
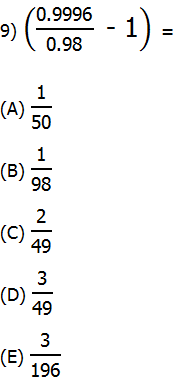
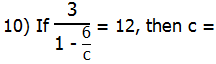
- (A) 2
(B) 4
(C) 6
(D) 8
(E) 12
Fractions and Decimals
I have already written a few blogs that would be germane to these topics.
1) Fractions: some of the basic ideas of fractions
2) Terminating and Repeating Decimals: an assortment of decimal ideas
3) Advanced Factoring: some sophisticated techniques for factoring ungainly looking decimals
More advanced ideas will be discussed the explanations to these problems, below.
Solutions to Practice Problems
1) First, let’s separate out the denominators and simplify them.
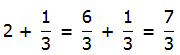
and
We are adding the reciprocals of these two fractions:
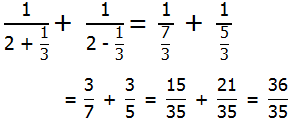
Answer = (E).
2) Let’s handle the numerator and denominator separately to begin. The number is the cube root of a decimal. The first thing we have to recognize is that 4 cubed is 64, so the cube root of 64 is 4. There are six total decimal places, so when we take a cube root, that will get divided by 3, down to only two decimal places. Thus,
The denominator is a little easier.
Those are the two numbers we have to divide. When divide decimals, we move both decimals an equal number of places to the right until the denominator is a whole number. Here, after we set up the fraction, we will have to move both decimals four places to the right, because the denominator starts with four decimal point.
Answer = (D).
3) There are a few different ways to think about this. First, I will multiply the entire inequality by positive 6. This will leave the direction of the inequality unchanged, and I can multiply right through the absolute value signs. This will eliminate any fractions.
|3y – 1| < 4
Well, the only way a thing can have an absolute value less than 4 is if it’s true value is between –4 and +4. Thus
–4 < 3y – 1 < 4
Add one to each term.
–3 < 3y < 5
Now, divide by +3. Because we are dividing by a positive, the direction of the inequalities stay the same.
So, y could be any positive or negative fraction between –1 and +1, so (B) & (C) & (D) are all allowed, and choice (E) is less than 5/3, so that’s also allowed. The only one that is not allowed is (A), and that’s the answer.
4) Notice that all the denominators are multiples of 30, so factor out a factor of 1/30:
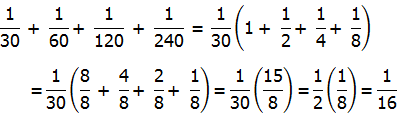
Answer = (B).
5) It’s actually better to change the decimals into fractions:
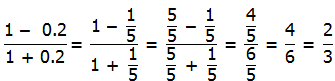
Answer = (B).
6) If you fill the 1/3 oz pipette and put this into the beaker. Then use the other pipette to remove 1/4 oz from the beaker. This 1/4 oz can be put back in the vat.
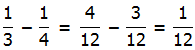
Thus, there would be 1/12 oz left in the beaker: that’s the amount that would have been transferred from the vat to the beaker.
If we repeat this same procedure, we will transfer another 1/12 oz from the vat to the beaker, and 2/12 = 1/6. Therefore, we could transfer either 1/12 or 1/6 from the vat to the beaker.
There is no way to transfer 1/7 to the beaker. No combination of arithmetic involving 1/3 and 1/4 will produce 1/7.
Answer = (C).
7) Let’s think about this is in stages. First, call the entire denominator D; then (0.2)/D = 4. From this, we must recognize that D must be 1/4 of 0.2, or D = 0.05.
Now, set that denominator equal to 0.05.
0.3 – x = 0.05
x = 0.3 – 0.05 = 0.25 = 1/4
Answer = (A).
8) Let’s make things easier by breaking this into two fraction. First, let’s work with 3.3 divided by 0.015. We will begin by sliding the decimals to the right a couple spaces:
Now, notice that the denominator is 3/2, so we will replace that decimal with the fraction:
That’s the first piece of the fraction. Now, consider the rest:
Multiply the pieces
(220)*(200) = 44,000
Answer = (D).
9) For this one, we need to use some advanced factoring. Notice that
0.9996 = 1 – 0.0004
Thus, we can express this as a difference of two squares, and use that to factor it
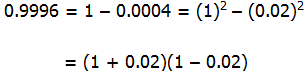
Now, consider that 0.98 = 1 – 0.02; then
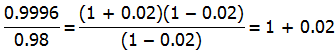
When we subtract 1, we get 0.02, which equals 1/50.
Answer = (A).
10) Think of this in stages. Call the denominator D. If 3/D = 12, then D must equal 1/4.
Now, look at the denominator. One minus thing equals 1/4, so that thing must equal 3/4.
Well, 6/c = 3/4, so c = 8.
Answer = (D).
