What are rates and ratios? How do rate and ratios problems differ? Hint: Not that much.

In fact, rates are just ratios in disguise. Here are a four GMAT practice problems exploring rates and ratios. Remember: no calculator!
Rates and Ratios Practice Problems
1) Someone on a skateboard is traveling 12 miles per hour. How many feet does she travel in 10 seconds? (1 mile = 5280 feet)
(A) 60
(B) 88
(C) 120
(D) 176
(E) 264
2) At 12:00 noon, a machine, operating at a fixed rate, starts processing a large set of identical items. At 1:45 p.m., the twenty-first item has just been processed, and 15 have not yet been processed. At what time will all 36 items be processed?
(A) 2:25 pm
(B) 3:00 pm
(C) 3:27 pm
(D) 4:13 pm
(E) 5:15 pm
3) An importer wants to purchase N high quality cameras from Germany and sell them in Japan. The cost in Germany of each camera is E euros. He will sell them in Japan at Y yen per camera, which will bring in a profit, given that the exchange rate is C yen per euro. Given the exchange rate of D US dollars per euro, and given that profit = (revenue) – (cost), which of the following represents his profit in dollars?
(A) N(YC – DE)
(B) ND(YC – E)
(C) ND((Y/C) – E)
(D) N((Y/C) – DE)
(E) ND(Y – E)/C
4) Machine A and machine B process the same work at different rates. Machine C processes work as fast as Machines A & B combined. Machine D processes work three times as fast as Machine C; Machine D’s work rate is also exactly four times Machine B’s rate. Assume all four machines work at fixed unchanging rates. If Machine A works alone on a job, it takes 5 hours and 40 minutes. If all four machines work together on the same job simultaneously, how long will it take all of them to complete it?
(A) 8 minutes
(B) 17 minutes
(C) 35 minutes
(D) 1 hour and 15 minutes
(E) 1 hours and 35 minutes
Solutions will come to these at the end of the article. Can’t contain your excitement? Click here to skip to the explanations.
Ratios and Proportions
Ratios are fractions. When we have an equation of the form fraction = fraction, that’s called a proportion. By far, the hardest part of dealing with a proportion is what you CAN and what you CAN’T cancel in a proportion. Many students are quite confused on this issue.
First of all, let’s be clear that cancelling is simply division. If I start with the fraction 24/32, and I “cancel the 8’s” to get 3/4, what I have really done is divide both the numerator and the denominator by 8. Similarly, if I have 5/35, and I cancel the 5’s, in the numerator, I am left with 1: the simplified version is 1/7. Too many student have the naïve view that canceling means “going away” or some other fairy-godmother operation. Instead, cancelling is a card-carrying legitimate mathematical operation, the operation of division.
Clearly, it’s always legitimate to cancel in the numerator and denominator of the same fraction, the same ratio, so of course we can do that on each side in a proportion.
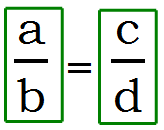
We might call that “vertical canceling” in a proportion: that’s 100% legal. The one that often surprises folks is what we might call that “horizontal canceling” in a proportion, which looks like this:
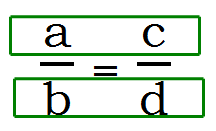
Canceling a common factor from a & c would simply involve dividing both sides of the equation by the same number, a 100% legal move. Similarly, canceling a common factor from b & d would simply involve multiplying both sides of the equation by the same number, another totally legal move. Even though “horizontal canceling” across the equal sign may look suspect, it’s totally valid.
Now, the one that causes real problems is what we might call “diagonal canceling,” because so many students seem to be under the impression that is this OK, but in fact, it’s 100% illegal and incorrect.
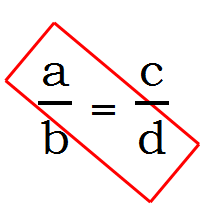

I suspect people confuse this with “cross-canceling” in the process of multiplying fractions. I actually abhor that uses term, “cross-canceling”: I think this term causes dozens of times more harm than good. If we were to perform the canceling of a with d, that would essential be equivalent to dividing one side of an equation by a number and multiply the other side of the equation by the same number! That’s not allowed! We always have to do the same thing to both sides! This is why this kind of “diagonal canceling” in a proportion is always disastrously incorrect.
OK, that’s the relevant mathematics without the real world stuff involved!
Rates
Rates are ratios, that is, fractions. Any fraction with different units in the numerator and in the denominator is a rate: miles per hour, $ per pound, grams per cubic centimeter, etc. Most rate questions can be solved by setting up a proportion. One common proportion type involves a (part)/(whole) on each side: for example, part of the job over all of the job, and part of the price or time over all of the price or time. In setting up any rate proportion, we have to make sure that units match: the same units in the two numerators, and the same units in the two denominators. The GMAT will expect you to know a few common unit changes (e.g. 1 hour = 60 min; 1 dozen items = 12 items, etc.); because some test-takers are familiar with metric and other are familiar with English, the GMAT most often would specify the conversion, as in #1 above. In any case, a GMAT rate problem often involves reconciling units differences in some way before we can do the math.
Another pertinent topic is that of work rates. Suppose Machine P does a job in 3 hours and Machine Q can do the same job in 6 hours. How fast would it take both machines working together? You see, we can’t add or subtract the times it takes to perform jobs. What we can add are the work rates! It doesn’t matter that these work rates would have the ambiguous units of “job/hour”—it doesn’t matter as long as every rate in the problem has the same units. The rate of P, job per time, would be 1/3, which means either one job every three hours or one-third of a job every hour: either is correct. Similarly, the rate of Q would be 1/6. We can’t add or subtract times, but we can add individual work rate to find a combined work rate. Adding fractions, we get (1/6) + (1/3) = (1/6) + (2/6) = 3/6 = 1/2. The combined rate of P & Q working together is 1/2, or one job per 2 hours. Thus, if P & Q were working together, it would take them just two hours to get the job done. That is the basic logic of work rates.
Rate and Ratios Summary
If you understand the rules of fractions and the concept of work rate, there’s nothing about rates and ratios you can’t understand. If you had any “aha” moments while reading this article, give the practice problems above another look before jumping in the solutions below.
Practice Problem Explanations
1) The speed is 12 mph. To change this to feet/second, we need to multiply by (5280 ft/mile), to cancel miles, and to multiply by (1 hour/3600 second) to cancel seconds.
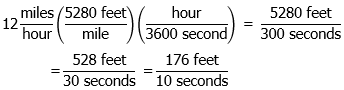
So, in 10 seconds, the skateboarder moves 176 feet. Answer = (D)
2) At 1:45, that is, 105 minutes after starting, the machine has completed 21/36 = 7/12 of the job. Let T be the whole time in minutes. For the total time, set up a proportion
![]()
Remember, with proportions, we can cancel a common factor in the two numerators; cancel the factor of 7.
![]()
Now, cross-multiply, and use the doubling & halving shortcut for multiplying.
T = 15*12 = 30*6 = 180
Now, 180 minutes = 3 hours, so the task finishes 3 hours later, at 3 p.m.
Answer = (B)
3) All the other currencies are related to euros, so we should focus on getting everything to euros and then changing it all at once to dollars.
Remember that profit = revenue – cost. For one camera, cost is E euros. The revenue of one camera is Y yen: let’s change that to euros, so that we can express cost, revenue, and profit all in euros.
We have an exchange rate of C yen/euro, with yen in the numerator and euros in the denominator. If we were to multiply this, we could cancel euros and wind up with yen. We don’t want that. We want to cancel yen and wind up with euros, so we need to divide by C. Y/C is the revenue of one camera in euros.
This means that ((Y/C) – E) is the profit in euros of one camera.
Now, the other exchange rate is D dollars/euro, with dollars in the numerator and euros in the denominator. If we multiply this, we cancel euros and get dollars. That’s exactly what we want. Thus, D((Y/C) – E) is the profit, in dollars, of one camera.
Now, just multiply by the number of cameras: ND((Y/C) – E)
Answer = (C)
4) Let A, B, C, and D be the rates of Machines A, B, C, and D respectively. We know that
(i) C = A + B
(ii) D = 3C
(iii) D = 4B
Starting with (ii) and (iii), equate the two expressions equal to D, and then substitute in the expression from (i) equal to C.
4B = 3C = 3(A + B) = 3A + 3B
B = 3A
Then, C = A + 3A = 4A, and D = 3*(4A) = 12A
The combined rate,
A + B + C + D = A + 3A + 4A + 12A = 20A
Since the combined rate is 20 times faster than Machine A alone, the combined time should be divided by 20.
Machine A alone takes 5 hr 40 min, or 340 minutes for the whole job. Divide this by 20:
340/20 = 17
The combination of the four machines will take 17 minutes to complete the job.
Answer = (B)
Editor’s Note: This post was originally published in August, 2014 and has been updated for freshness, accuracy, and comprehensiveness.






Leave a Reply