First, a few practice problems. Remember: no calculator!
1) If $5,000,000 is the initial amount placed in an account that collects 7% annual interest, which of the following compounding rates would produce the largest total amount after two years?
(A) compounding annually
(B) compounding quarterly
(C) compounding monthly
(D) compounding daily
(E) All four of these would produce the same total
2) If A is the initial amount put into an account, R is the annual percentage of interest written as a decimal, and the interest compounds annually, then which of the following would be an expression, in terms of A and R, for the interest accrued in three years?
3) At the beginning of January 2003, Elizabeth invested money in an account that collected interest, compounding more frequently than a year. Assume the annual percentage rate of interest remained constant. What is the total amount she has invested after seven years?
Statement #1: her initial investment was $20,000
Statement #2: the account accrued 7% annual interest
4) Sarah invested $38,700 in an account that paid 6.2% annual interest, compounding monthly. She left the money in this account, collecting interest for a full three-year period. Approximately how much interest did she earn in the last month of this period?
(A) $239.47
(B) $714.73
(C) $2793.80
(D) $7,888.83
(E) $15,529.61
Solutions to these will be given at the end of the article.
Simple Interest
In grade school, you learn about simple interest, largely because we want to teach little kids something about the idea of interest, and that’s the only kind of interest that children can understand. No one anywhere in the real world actually uses simple interest: it’s a pure mathematical fiction.
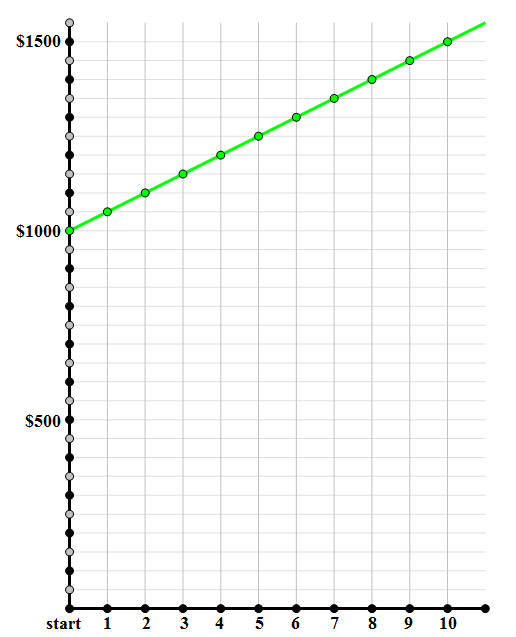
Here’s how it works. There’s an initial amount A, and an annual percentage P. At the end of each year, you get interest in the amount of P percent of A — the same amount every year. Suppose the initial amount is $1000, and the annual percentage is 5%. Well, 5% of $1000 is $50, so each year, you would get the fixed value of $50 in interest. If you plotted the value of the account (principle + interest) vs. time, you would get a straight line.
Again, this is a fiction we teach children, the mathematical equivalent of Santa Claus. This never takes place in the real world.
Compound Interest, compounding annually
With compound interest, in each successive year or period, you collect more interest not merely on the principle but on all the interest you have accrued up to that point in time. Interest on interest: that’s the big idea of compound interest.
Here’s how it plays out. Again, there’s an initial amount A, and an annual percentage P, and we also have to know how frequently we are compounding. For starters, let’s just say that we are compounding annually, once a year at the end of the year. In fact, let’s say we have $1000, and the annual interest rate is 5%. Well, in the first year, we would earn five percent on $1000, and gain $50 in interest. The first year is exactly the same as the simple interest scenario. After that first year, we now have $1050 in the account, so at the end of the second year, we gain 5% of $1050, or $52.50, for a new total of $1102.50. Now, that’s our new total, so at the end of the third year, we gain 5% of $1102.50, or $55.12 (rounded down to the nearest penny), for a new total of $1157.62. At the end of three years, the simple interest scenario would give us $1150, so the compound interest gains us an extra $7.62 —- not much, but then again, $1000 is not a lot to have invested. You can see that, with millions or billions of dollars, this would be a significant difference.
Here, I was demonstrating everything step-by-step for clarity, but if we wanted to calculate the total amount after a large number of years, we would just use a formula. We know that each year, the amount increased by 5%, and we know that 1.05 is the multiplier for a 5% increase. After 20 years, the amount in the account would have experienced twenty 5% increases, so the total amount would be
We don’t have to do it step-by-step: we can just jump to the answer we need, using multipliers. Of course, for this exact value, we would need a calculator, and you don’t get a calculator on the GMAT Quantitative section. Sometimes, though, the GMAT lists some answers in “formula form”, and you would just have to recognize this particular expression, 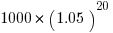 , as the right formula for this amount.
, as the right formula for this amount.
If we graph compound interest against time, we get an upward curving graph (purple), which curves away from the simple interest straight line (green):
The curve of the graph, that is to say, the multiplying effect of the interest, gets more pronounces as time goes on.
BIG IDEA #1: as long as there is more than one compounding period, then compound interest always earns more than simple interest.
Other compounding periods
A year is a long time to wait to get any interest. Historically, some banks have compounded over shortened compounding period. Here is a table of common compounding periods:
Technically, the fraction for “compounding daily” would be 1/365 in a non-leap year and 1/366 in a leap year; alternatively, one could use 1/365.25 for every year.
Now, how does this work? Let’s say the bank gives 5% annual, compounding quarterly. It would be splendid if the bank wanted to give you another 5% each and every quarter, but that’s not how it works. The bank takes the percentage rate of interest and multiplies it by the corresponding fraction. For 5% annual, compounding quarterly, we would multiply (5%)*(1/4) = 1.25%. That’s the percentage increase we get each quarter. The multiplier for a 1.25% increase is 1.0125. Suppose we invest $1000 initially and keep the money in this account for seven years: that would be 7*4 = 28 compounding periods, so there are twenty-eight times in that period in which the account experiences a 1.25% increase. Thus, the formula would be
For compounding quarterly, we divide the annual rate by four and compound four times each year. For compounding monthly, we divide the annual rate by twelve and compound twelve times a year. Similarly, for daily or any other conceivable compounding period.
How do the amounts of interest accrued compare for different compounding periods? To compare this, let’s pick a larger initial value, $1,000,000, and collect over a longer period, 20 years. Below are the total amounts, after twenty years, on an initial deposit of one million dollars compound at 5% annual:
- simple interest = $2,000,000
- compounding annually = $2,653,297.71
- compounding quarterly = $2,701484.94
- compounding monthly = $2,712,640.29
- compounding daily = $2,718,095.80
- compounding hourly = $2,718,274.07
As we go down that list, notice the values keep increasing as we decrease the size of the compounding period (and, hence, increase the total number of compound periods). This leads to:
BIG IDEA #2: We always get more interest, and larger account value overall, when the compounding period decreases; the more compounding periods we have, the more interest we earn.
Admittedly, the difference between “compounding daily” and “compounding hourly” only turn out to be a measly $178 on a million dollar investment over a twenty year period. A infinitesimally small difference, but technically, it is still an increase to move from “compounding daily” to “compounding hourly.”
Both ways
Notice that so far, we have been talking about investments and interest that you earn. All of this, everything in this article, works equally well for debt and interest that you have to pay. Just as the compounding effect, over time, magically multiplies an investment, so the same compounding effect will sink you deeper and deeper into debt. This, in a nutshell, is the lose-lose proposition of credit card debt.
A little more than you need to know …
You may have noticed that, as the compounding periods get smaller and smaller, the amount increase in every diminishing steps. In fact, as you may suspect, the total amount you possibly could earn from decreasing the compound period reaches a ceiling, a limit. This limit is called “compounding continuously.” The mathematics of this involves the special irrational number e, named for Leonard Euler (1707 – 1783), who is often considered the single greatest mathematician of all times.
e = 2.71828182845904523536028747135266249775724709369995 …
The formula for calculating continuously compound interest involves e, and is more complicated than anything you need to understand for the GMAT. I will simply point out, in the example above, with one million dollars invested at 5% annual for 20 years, the limit of continuously compounding would be 1 million times e, which is $2,718,281.83. You do not need to understand why that is or how this was calculated.
Most banks use monthly compounding interest, for accounts and for mortgages: this make sense for accounts with monthly statement or payments. Credit cards tend to use continually compounding interest, because charges or payments could occur at any point, at any time of any day of the month. In addition to understanding the mathematics of compound interest, it’s good to have a general idea of how it works in the real world: after all, the history or logic of compound interest would be a very apt topic for a Reading Comprehension passage or a Critical Reasoning prompt on the GMAT!
Summary
If you had any “aha’s” while reading this article, you may want to go back a take another look at the four practice problems above. If you would like to express anything on these themes, or if you have a question about anything I said in this article, please let us know in the comments section.
Practice problem explanations
1) The smaller the compounding period is, the greater the number of times the interest will be compounded. Of course, if we compound monthly instead of quarterly, then we are compounding by 1/12 of the annual rate each time, instead of 1/4. The number of times we compound goes up, but the percentage by which we compound each time goes down. Naively, you may think that those two would cancel out, but they don’t. As discussed above, as the compounding period gets smaller, the total amount of interest earned goes up. Therefore, we will get the most with the smallest compound period, daily. Answer = (D)
2) Notice that, since R is the annual percent as a decimal, we can form a multiplier simply by adding one: (1 + R). That’s very handy! We will explore two different methods to get the answer.
Method One: Step-by-step
Starting amount = A
After one year, we multiply by the multiplier once
That’s the total amount at the end of the first year. The amount A is the original principle, and AR is the interest earned.
At the end of the second year, that entire amount is multiplied by the multiplier. We need to FOIL.
That’s the total amount at the end of the second year. The amount A is the original principle, and the rest is the interest earned.
At the end of the third year, this entire amount is again multiplied by the multiplier.
That’s the total amount at the end of the third year. The amount A is the original principle, and the rest is the interest earned.
Answer = (C)
Method Two: some fancy algebra
Over the course of three years, the initial amount A is multiplied by the multiplier (1 + R) three times. Thus, after three years,
Now, if you happen to know it offhand, we can use the cube of a sum formula:
Thus,
and
Answer = (C)
3) In order to determine the total amount at the end of an investment, we would need to know three things: (a) the initial deposit; (b) the annual percentage rate; and (c) the compounding period.
Statement #1 tells us the initial deposit but not the annual percentage rate. Insufficient.
Statement #2 tells us the annual percentage rate but not the initial deposit. Insufficient.
Together, we know both the initial deposit and the annual percentage rate, but we still don’t know the compounding period. All we know is that it’s less than a year, but quarterly compounding vs. monthly compounding vs. daily compounding would produce different total amounts at the end. Without knowing the exact compounding period, we cannot calculate a precise answer. Even together, the statements are insufficient.
Answer = (E)
4) Without a calculator available, this is a problem screaming for estimation. The problem even uses the magic word “approximately” to indicate that estimation is a good idea, and the answer choices are spread far apart, making it easier to estimate an individual answer.
Let’s round the deposit up to $40,000, and the percentage down to 6% annual. Compounding monthly means each month, Sarah will accrue 6/12 = 0.5% in interest. Well, 1% of $40,000 is $400. Divide by 2: then 0.5% of $40,000 would be $200. That would be the simple interest amount, as well as the interest in the first month. We expect the amount in the last month to be a little more than this, but certain not even as large as double this amount. The only possible answer is (A).



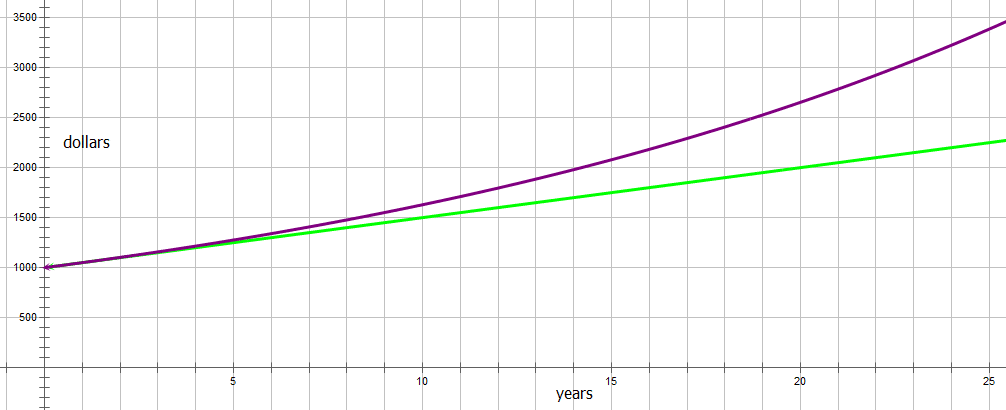
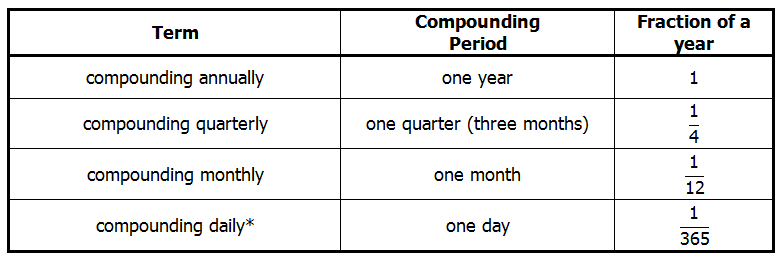

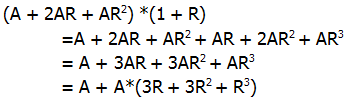




Leave a Reply