Learn this technique to master set questions of GMAT Math word problems.
Practice questions
First, try these challenging practice questions.
1) Of the 80 houses in a development, 50 have a two-car garage, 40 have an in-the-ground swimming pool, and 35 have both a two-car garage and an in-the-ground swimming pool. How many houses in the development have neither a two-car garage nor an in-the-ground swimming pool?
A. 10
B. 15
C. 20
D. 25
E. 30
2) A certain school has three performing arts extracurricular activities: Band, Chorus, or Drama. Students must participate in at least one, and may participate in two or even in all three. There are 120 students in the school. There are 70 students in Band, 73 in the Chorus, and 45 in the Drama. Furthermore, 37 students are in both the Band and Chorus, 20 are in both the Band and the Drama, and 8 students are in all three groups. Twenty-five students are just in the chorus, not in anything else. How many students participate in only the drama?
A. 11
B. 12
C. 14
D. 17
E. 21
Introduction to sets
The idea of a set is, in some sense, the most fundamental idea in all of mathematics. Nonetheless, it’s a very simple idea. A set is simply a collection of objects or elements. When the members of a set are all numbers, then we use “set notation”, which consists of brackets. For example:
A = {2, 3, 3, 5, 7}
That notation denotes set A with five numerical members. When all the members of the set are numbers, typical questions involve computations like the mean or the median: here, the mean (or average) of set A is 4, and the median of A is 3. You can read more about those calculations at this post.
Overlapping sets
Numerical sets can be handled with statistical calculations. Non-numerical sets, sets in which the members are people or cars or companies, are the stuff of tricky word problems. Ordinarily, there’s nothing particular challenging if there’s only one set: some of the people are in that set, whatever it is, and the rest aren’t. No challenge.
Things get more interesting if there are two or more overlapping sets. For example, in the SF Bay Area, many adult residents were born out of state — many, but not all; many adult residents have a college education — many, but not all; and many adult residents are SF Giants fans — many, but not all. Those are three overlapping sets —- any particular adult resident of the SF Bay Area many be a member of none, one, two, or all three of those three categories. As it happens, I am a member of exactly two of those categories. This is exactly the situation of the practice questions posed above.
Venn diagrams
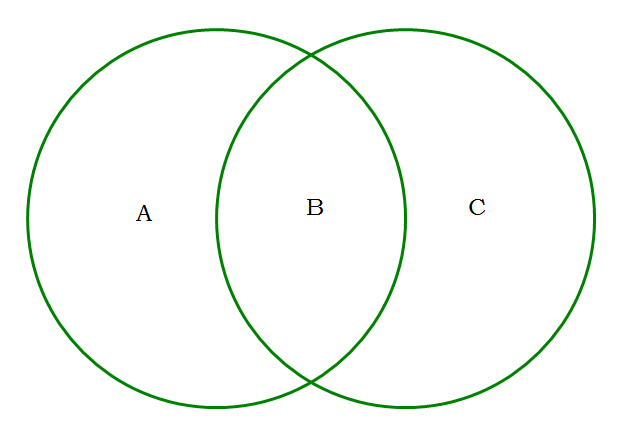
Venn diagrams are the best method for untangling overlapping sets. If you have two overlapping sets, you need a two-circle Venn diagram:
This diagram contains three discrete regions:
A = those elements in just the left circle
B = those element in both categories, in the overlap
C = those elements in just the right circle
There may also be a fourth discrete region, those elements that are not members of any set. Typically, the problem will only give us information about totals — the total number of elements altogether, the total number in each circle, and the overlap. If you are told there are 70 members in the right circle, and 20 members in the overlap, then you would know B + C = 70 and B = 20, so from that you could deduce C = 50, the number of elements that are just in the portion of the circle labeled C. In general, you work from the center outward, figuring out one discrete region after another. Once you know the value of each individual discrete region, you will be able to answer any question about the number in any particular grouping.
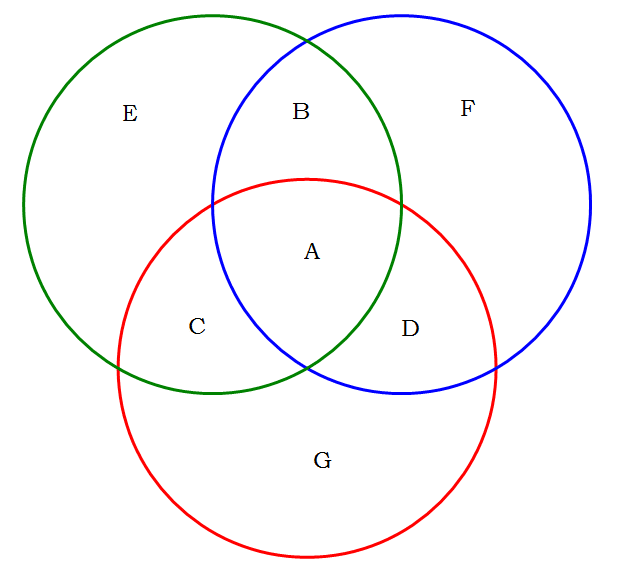
If there are three overlapping categories, we use a three-circle Venn diagram:
This diagram has at least seven discrete regions
A = members of all three circles
B = members of the green and blue circles, but not the red circle
C = members of the green and red circles, but not the blue circle
D = members of the blue and red circles, but not the green circle
E = members of the green circle but of neither the blue nor the red circles
F = members of the blue circle but of neither the green nor the red circles
G = members of the red circle but of neither the green nor the blue circles
Depending on context, there may also be a eighth discrete region, those elements that are not members of any of the three set. Typically, the problem will only give us information about totals. This gets very tricky. If we are told the total in any one circle, that includes four discrete regions; for example, the green circle includes A + B + C + E. Similarly, the overlap of two circles contains two discrete regions: for example, the overlap of the blue and red circles includes A + D. The problem will always tell you how many elements are in the central region (A), and will often tell you how many are in each circle, and how many in each overlap of two circles. In general, you work from the center outward, figuring out one discrete region after another. Once you know the value of each individual discrete region, you will be able to answer any question about the number in any particular grouping.
With these strategies, you may find the practice problems at the beginning somewhat more approachable. Try them again, before reading the explanations below.
In the next post, we will look at set problems in which each element is categorized according to two different variables at once.
Practice question explanations
1) Here, we have two categories: (a) with or without two-car garage, and (b) with or without an in-the-ground pool. Houses can be members of either, both, or neither category. We will use a two circle Venn diagram:
We know the total of the group is 80 —– A + B + C + D = 80. We know the green circle, two-car garages, has 50 members, so A + B = 50. We know the blue circle, in-the-ground pool, has 40 members, so B + C = 40. We also know the crucial overlap region, B = 35. If B = 35, in the green circle, we can deduce that A = 15, and in the blue circle, we can deduce that C = 5. Then
A + B + C + D = 15 + 35 + 5 + D = 80
D = 25
Thus, 25 houses in this development have neither a two-car garage nor an in-the-ground swimming pool. Answer = D.
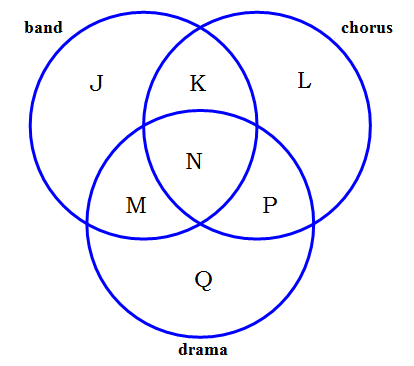
2) Here, we have three categories, so we need three circles. Every student must take at least one of these three performing arts extracurricular activities, so there will be no one outside the three circles.
The sum of all seven = 120 (we never use this number in this question)
The totals for the band (70), the chorus (73), and the drama (45) each involve the sum of four discrete regions. We will have to find other information before we can employ them.
“8 students are in all three groups”
N = 8.
“37 students are in both the Band and Chorus”
37 = K + N = K + 8 —> K = 29
“20 are in both the Band and the Drama”
20 = M + N = M + 8 —> M = 12
“twenty-five students are just in the chorus, not in anything else”
L = 25
We now have identified three of the regions in the Chorus circle, so we can solve for P.
chorus = 73 = K + L + N + P
73 = 29 + 25 + 8 + P
P = 11
Now, we have identified three of the regions in the Drama circle, so we can solve for Q.
drama = 45 = M + N + P + Q
45 = 12 + 8 + 11 + Q
Q = 14
This is precisely what the question was asking: how many students are only in drama? There are 14 students who take only drama.
Answer = C







Leave a Reply