Master these seemingly intimidating mathematical symbols!
Practice Questions
First, try these practice questions.
1) The numbers a, b, and c are all non-zero integers. Is a > 0?
Statement #1: 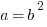
Statement #2: 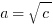
2) The numbers a, b, and c are all non-zero integers. Is a > 0?
Statement #1: 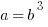
Statement #2: 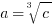
Square Roots
When you square a number, you are multiplying it by itself, e.g. 6*6 = 36. When you take the square-root of a number, you are undoing the square, going backwards from the result of squaring to the input that was originally squared: 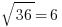 . Similarly, 8*8 = 64, so
. Similarly, 8*8 = 64, so 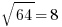 . As long as all the numbers are positive, everything is straightforward.
. As long as all the numbers are positive, everything is straightforward.
It’s easy to find the square root of a perfect square. All other square roots are ugly decimals. For estimation purposes on the very hardest GMAT questions, it might be useful to memorize that 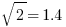 and
and 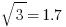 , but without a calculator, no one is going to ask you to calculate the values of any decimal square roots bigger than that. If something like
, but without a calculator, no one is going to ask you to calculate the values of any decimal square roots bigger than that. If something like 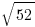 shows up, all you have to recognize is between what integers you would find that decimal. For example,
shows up, all you have to recognize is between what integers you would find that decimal. For example,
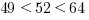
therefore
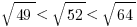
therefore
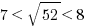
It’s also good to know how to simplify square roots.
The Symbol: Positive or Negative?
What is the name of this symbol? The benighted unwashed masses will call this simply the “square root symbol”, but that’s not the full story. The technical name is the “principal square root symbol.” Here, “principal” (in the sense of “main” or “most important”) means: take the positive root only.
This thickens the plot. The equation 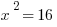 has two solutions, x = +4 and x = -4, because
has two solutions, x = +4 and x = -4, because 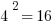 and
and 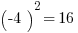 , and the GMAT will impale you for only remembering one of those two. At the same time,
, and the GMAT will impale you for only remembering one of those two. At the same time, 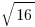 has only one output:
has only one output: 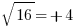 only. When you yourself undo a square by taking a square root, that’s a process that results in two possibilities, but when you see this symbol as such, printed as part of the problem, it means find the positive square root only.
only. When you yourself undo a square by taking a square root, that’s a process that results in two possibilities, but when you see this symbol as such, printed as part of the problem, it means find the positive square root only.
Notice that we can take the square root of zero: 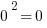 , so
, so 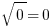 , perfectly legal. Notice, also, we cannot take the square root of a negative — for example,
, perfectly legal. Notice, also, we cannot take the square root of a negative — for example, 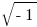 — because that involves leaving the real number line. There are branches of math that do this, but it’s well beyond the scope of the GMAT.
— because that involves leaving the real number line. There are branches of math that do this, but it’s well beyond the scope of the GMAT.
Cubes and Cube Roots
When we raise a number to the third power, 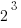 , that is called “cubing” it (because if we had a cube of side = 2, then the “cube” of that number would equal the volume of the cube). Here,
, that is called “cubing” it (because if we had a cube of side = 2, then the “cube” of that number would equal the volume of the cube). Here, 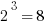 . A cube root simply undoes this process:
. A cube root simply undoes this process: 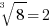 . As with a square roots, it’s easy to find the cube roots of perfect cubes, and on the GMAT you would never be expected to find an ugly decimal cube root without a calculator.
. As with a square roots, it’s easy to find the cube roots of perfect cubes, and on the GMAT you would never be expected to find an ugly decimal cube root without a calculator.
Cubes and cube roots with negatives get interesting. While 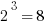 , it turns out that
, it turns out that 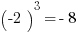 . When you multiply two negatives you get a positive, but when you multiply three negatives, you get a negative. More generally, when you multiply any even number of negatives you get a positive, but when you multiply any odd number of negatives, you get a negative. Therefore, when you cube a positive, you get a positive, but if you cube a negative, you get a negative.
. When you multiply two negatives you get a positive, but when you multiply three negatives, you get a negative. More generally, when you multiply any even number of negatives you get a positive, but when you multiply any odd number of negatives, you get a negative. Therefore, when you cube a positive, you get a positive, but if you cube a negative, you get a negative.
This means: while you can’t take the square root of a negative, you certainly can take the cube root of a negative. Undoing the equation 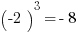 , we get
, we get 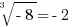 . In general, the cube root of a positive will be positive, and the cube root of a negative will be negative.
. In general, the cube root of a positive will be positive, and the cube root of a negative will be negative.
It can also be a time-saver to remember the first five cubes:
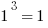
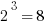
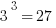
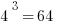
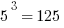
You generally will not be expected to recognize cubes of larger numbers. Knowing just these will translate handily into all sorts of related facts: for example, 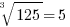 and
and 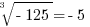 .
.
If you remember just this, you will be well-prepare for whatever the GMAT asks you about roots.
Additional Practice Question
3) http://gmat.magoosh.com/questions/91
Explanations of the Practice Questions
1) All that is given in the prompt is that a, b, and c are non-zero integers.
Statement #1: the result of square anything is always positive, so whether b is negative or positive, a must be positive. This statement, by itself, is sufficient.
Statement #2: since the square root symbol is printed as part of the problem, the output of the sqrt{c} must be positive. We know for a fact that a must be positive. Again, this statement, by itself, is sufficient.
Both statements are sufficient. Answer = D.
2) Again, all that is given in the prompt is that a, b, and c are non-zero integers.
Statement #1: now, if we cube a positive, we get a positive, but if we cube a negative, we get a negative. The numbers a & b are either both positive or both negative, but since we don’t know the sign of b, we cannot determine the sign of a. This statement, by itself, is insufficient.
Statement #2: if we take the cube root of a positive, we will get a positive, but if we take the cube-root of a negative, we get a negative. The numbers a & c are either both positive or both negative, but since we don’t know the sign of c, we cannot determine the sign of a. This statement, by itself, is insufficient.
Combined Statements: If we put both statements together, we get that all three numbers, a, b, and c, have to have the same sign: either all three are positive, or all three are negative. We have no further information that would allow us to determine which of those two is the case. Thus, even with combined statements, we still do not have enough information to give a definitive answer to the prompt question. Combined, the statements are still insufficient. Answer = E





Leave a Reply