A Case Study of the Area of an Equilateral Triangle
Fact: on the GMAT Math section, you are likely to find questions about the area of an equilateral triangle, and it would be efficient if you knew the formula. (BTW, the formula appears a little further below.)
Don’t Merely Memorize
I am going to recommend that you work to remember this formula, rather than memorize it. What distinction am I drawing? By memorizing, I mean you write this isolated factoid, area of an equilateral triangle, on an index card, and drill yourself until you can successful regurgitate it. That’s one way to get something into your memory, but it’s hard to retain it, particularly over the long term. One big problem is: on the day of the test, because of increased stress, if you forget the factoid you previously could regurgitate, you are stuck: you have no recourse.
Memory with Contextual Understanding
By contrast, true learning involves remembering something because you understand it. When you understand every step of an argument and how it fits together, that makes it very easy to remember. This is particularly true in mathematics: if you can remember the series of steps that lead to a conclusion, first of all, such learning makes the conclusion much easier to remember; furthermore, even if you can’t remember the conclusion or want to check it, you will probably remember enough of the argument that you can reconstruct it if need be. This is a much deeper kind of understanding.
Example: The Area of an Equilateral Triangle
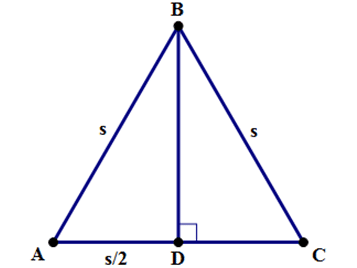
Suppose you have an equilateral triangle with sides of length s.
We know all the sides have the same length. It’s not relevant for finding the area, but we also know that all three angles equal 60 degrees.
Step #1: We know that the formula for the area of a triangle is 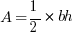 . The base is clearly s, but we need a height.
. The base is clearly s, but we need a height.
Step #2: We draw an altitude, that is, a line from B that is perpendicular to AC. The length of this line is the height needed in A = 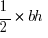 .
.
Step #3: Point D is the midpoint of AC, so AD = s/2. Also, angle ADB is 90 degrees.
Step #4: Call the length of BD h, and apply the Pythagorean Theorem in triangle ADB:
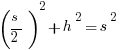
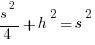
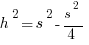
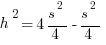
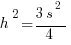
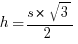
Step #5: Now that we have the height in terms of s, we can find the area.
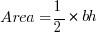
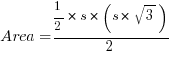
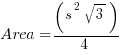
That last formula is, indeed, the area of an equilateral triangle, and remembering it will be a definite time-saver on GMAT Math. Again, I don’t want you to memorize it. Rather, I strongly encourage you to remember this five step argument: practice recreating it step-by-step until you can flawlessly recapitulate the entire thing by yourself. Then, you won’t merely remember this formula — you will own it!
I encourage you to do that with each important GMAT math formula. If you don’t know the steps that lead to a particular formula, and can find it online, leave me a comment :).
Try a free Magoosh GMAT Practice Question to practice “remembering” what we just learned!






Leave a Reply