First, some practice questions. The scenario below is relevant to questions #1-#3.
There are two sets of letters, and you are going to pick exactly one letter from each set.
Set #1 = {A, B, C, D, E}
Set #2 = {K, L, M, N, O, P}
1) What is the probability of picking a C and an M?
-
(A) 1/30
(B) 1/15
(C) 1/6
(D) 1/5
(E) 1/3
2) What is the probability of picking a C or an M?
-
(A) 1/30
(B) 1/15
(C) 1/6
(D) 1/5
(E) 1/3
3) What is the probability of picking two vowels?
-
(A) 1/30
(B) 1/15
(C) 1/6
(D) 1/5
(E) 1/3
_____________________________________________________________________
4) In a certain corporation, there are 300 part-time employees and 100 full-time employees. It is known that 20% of the part-time employees have advanced degrees and 40% of the full-time have advanced degrees. If one of the 400 employees is chosen at random, what is the probability this employee has an advanced degree and is a full-time employee?
-
(A) 1/20
(B) 1/10
(C) 1/5
(D) 2/5
(E) 3/4
5) In a certain corporation, there are 300 part-time employees and 100 full-time employees. It is known that 20% of the part-time employees have advanced degrees and 40% of the full-time have advanced degrees. If one of the 400 employees is chosen at random, what is the probability this employee has an advanced degree or is a full-time employee?
-
(A) 1/20
(B) 1/10
(C) 1/5
(D) 2/5
(E) 3/4
The simplistic probability rules
Here is the absolute bare minimum you need to know for probability calculations on the GMAT:
“AND” means MULTIPLY
“OR” means ADD
Is this the whole story? Well, not exactly. But if you can’t remember or don’t understand anything else about probability, at least know these two bare-bones rules, because just this will put ahead of so many people. Just this is enough to solve the problems #1 and #3, although these alone could lead to problems on the others. Before we qualify these simplistic rules, we need to discuss two distinctions.
Disjoint
Two events are disjoint if they are mutually exclusive. In other words, two events are disjoint if the probability of their simultaneous occurrence is zero, that is, it is absolutely impossible to have them both happen at the same time. For example, different faces of a single die are disjoint: under ordinary circumstances, if you roll one die once, you can’t simultaneously get, say, both a 3 and a 5. Those two are disjoint. Suppose we are picking random people and classifying them by their current age. In this process, being in the category “teenager” and being in the category “senior citizen” are disjoint: there is no one we could pick who is simultaneously in both categories. Most categories involving human beings are too messy for the distinction “disjoint” to apply.
If events A and B are disjoint, then we can use the simplified OR rule:
P(A or B) = P(A) + P(B)
That’s the case in which the simplified rule, OR means ADD, works perfectly. If events A and B are not disjoint, then we have to use the generalized OR rule:
P(A or B) = P(A) + P(B) – P(A and B)
The reason for that final term: we need to subtract the overlap. The events in the region “A and B” are included in region A and also in region B, so if we add those two regions, the overlap gets counted twice. We need to subtract it, so it is only counted once like everything else.
Independent
Two events are independent if whether one happens has absolutely no influence on whether the other happens. In other words, knowing about the outcome of one event gives absolutely no information about how the other event will turn out. For example, if I roll two ordinary dice, the outcome of each die is independent of the other die. If I tell you I rolled two dice, and the first die was a 4, then knowing that give you no clue about what the number on the other die might be. On any given day, what the weather is in the San Francisco Bay Area and how the Dow Jones Industrial Average performs are independent: knowing one gives us absolutely no information about how the other turned out.
We have to be careful. If I shuffle a deck of cards, draw one, replace it, re-shuffle, and draw another, then the two cards are independent. BUT, if I shuffle the deck, draw one card, and then without replacement draw a second card, then they are not independent. For example, if the first card is the 7 of Hearts, then it is less likely that the second card would be either a 7 or a Heart, because there are fewer of those options among the remaining 51 cards.
Also, notice that there are many human situations which would be independent in a perfect just ideal world, but regrettably are not independent in a real world full of inequities. In a perfect world, gender and corporate promotion would be independent, but in practice, they are not. In a perfect world, race and criminal conviction would be independent, but in practice, they are not.
If events A and B are independent, then we can use the simplified AND rule:
P(A and B) = P(A)*P(B)
That’s the case in which the simplified rule, AND means MULTIPLY, works perfectly. If events A and B are not independent, then things get complicated. Technically, the “generalized AND rule” formula would involve a concept known as “conditional probability“, which would lead into realms of probability theory that are tested less frequently on the GMAT. See that other blog that discusses conditional probability if you want to understand this advanced topic in more detail.
Practice
Having read this post, take another look at those practice questions, and see if you understand them better, before simply reading the explanations below. Be patient with yourself as you work through probability: it takes time to internalize these distinctions, such as “disjoint” and “independent”. There will be more information in the next post in this sequence.
Practice problem solutions
1) Whatever we pick from the first set is independent with whatever we pick from the second set, so we can use the simplified AND rule.
P(first pick = C) = 1/5
P(second pick = M) = 1/6
P(C and M) = P(C)*P(M) = (1/5)*(1/6) = 1/30
Answer = A
2) Picking an M is not disjoint with picking a C — they both could happen on the same round of the game. We have to use the generalized OR rule for this:
P(C or M) = P(C) + P(M) – P(C and M)
Fortunately, we know the first two, and we calculated the value of the third term already in #1.
P(C or M) = P(C) + P(M) – P(C and M)
Answer = E
3) On the first pick, two of the five letters are vowels — A & E — so the probability of picking a vowel on the first pick is 2/5. On the second pick, only one letter out of the six is a vowel — O — so the probability of picking a vowel on the second pick is 1/6. The two picks are independent: what one selects from one set has absolutely no bearing on what one picks from the other set. Therefore, we can use the generalized AND rule.
P(two vowels) = P(vowel on first pick)*P(vowel on second pick) =(2/5)*(1/6) = 2/30 = 1/15
Answer = B
4) Here we have an AND question, and the parameters — full-time and advanced degree — are not independent. If I tell you the status of a certain employee, then that gives me information about how likely it is that this employee has an advanced degree. One parameter gives information about the other, which means they are not independent. Therefore, we cannot use the simplified AND rule. Fortunately, it is relatively easy here to calculate everything directly.
There are 100 full-time employees, and we know 40% of them have advanced degrees, so there are 40 employees who both are full-time and have an advanced degree. That’s the number of employees in the AND region. Well, there are 400 employees altogether. Of these 400 total employees, the probability of picking someone in this AND region is
P = 40/400 = 1/10
Answer = B
5) In this corporation, there are 400 total employees. There are 100 full-time. Of the 300 part-time, 20% have advanced degrees —-10% of 300 must be 30, so 20% of 300 must be 60. Add the full-time employees and the part-time employees with advanced degrees: 100 + 60 = 160. This is the OR region, full set of individuals that satisfy the condition “has an advanced degree or is full-time.” Of the 400 employees, what’s the probability of picking one of the 160 in this particular group?
P = 160/400 = 16/40 = 4/10 = 2/5
Answer = D
Try out some more GMAT probability problems here.
Special Note:
To find out where probability sits in the “big picture” of GMAT Quant, and what other Quant concepts you should study, check out our post entitled:
What Kind of Math is on the GMAT? Breakdown of Quant Concepts by Frequency

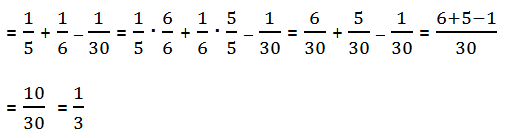




Leave a Reply