
This is an extremely difficult question category that appears only infrequently on the GMAT. First, a couple of GMAT algebra practice problems.

1) The dark purple region on the number line above is shown in its entirety. This region is delineated by which of the following inequalities?
(A) 10 < |x + 10| < 80
(B) 10 < |x – 100| < 80
(C) |x – 20| < 70
(D) |x – 20| < | x – 90|
(E) |x – 55| < 35
2) If |x| < 20 and |x – 8| > |x + 4|, which of the following expresses the allowable range for x?
(A) –12 < x < 12
(B) –20 < x < 2
(C) –20 < x < –12 and 12 < x < 20
(D) –20 < x < –8 and 4 < x < 20
(E) –20 < x < –4 and 8 < x < 20
3) If |(x – 3)2 + 2| < |x – 7| , which of the following expresses the allowable range for x?
(A) 1 < x < 4
(B) 1 < x < 7
(C) – 1 < x < 4 and 7 < x
(D) x < – 1 and 4 < x < 7
(E) – 7 < x < 4 and 7 < x
Explanations to these will follow the discussion.
A hard question type
I want to make clear that this question type is very tricky, something that might pose challenges even to students relatively strong in math. I also want to make clear that we could send 50 people to take 50 separate GMATs, and it may be that not one of them would see such a question on their GMAT. This is a very infrequent question genre, and it would only be asked if you were acing the Quant sections and the CAT were throwing everything including the kitchen sink at you!
If you find what I say in this blog article helpful, that’s great: it may give you some insight into other, easier questions involving absolute values and/or inequalities. If you are still confused, don’t worry: you are rather unlikely to see this question type on test day.
Thinking about absolute values
Fundamentally, the absolute value is about distance, and thinking about it geometrically is often the key to difficult absolute value questions. The naïve understanding of absolute value is that it “makes things positive.” While this is undeniably true, it is not always the most mathematically productive way to understand the concept. It’s undeniably true that |+5| = +5 and that |-5| = +5. We could say that both are true because the absolute value “makes everything positive,” or we could say that these two numbers, +5 and –5, have a distance of 5 from zero on the number line.
This geometric interpretation about distance becomes considerably more important when we are dealing with algebra. The expression |x| is the distance from x to zero. The expression |x – 6| is the distance from x to +6. The expression |x + 2| is the distance from x to – 2: to understand this, remember that x + 2 = x – (– 2). In general, the expression |x – c| is the distance from any x to the fixed point x = c.
This distance interpretation replaces a whole lot of complicated calculations. For example, if we had to solve the inequality |x – 10| ≥ |x – 20|, that’s just saying that the distance from x to 20 is smaller than the distance from x to 10—in other words, x is closer to 20 than to 10, and because of the “or equal” part, it could be an equal distance also. Well, the point x = 15 is the only point on the number line that is equidistant from x = 10 and x = 20. If x has to be either an equal distance from 10 and 20, or closer to 20, then it has to be at the point x = 15 or to the right. Any point between 15 and 20 is closer to 20 than to 10, and any point to the right of 20 has to be closer to 20 than to 10. Thus, the solution is 15 ≤ x.

What region is denoted by the inequality |x – 25| > 10? Well, all we are saying is that we have to be more than 10 units away from the point x = 25. If we go 10 units to the left, we get to x = 15: we can’t be here, at a distance equal to 10, but we could be the left of x = 15, at a distance of more than 10. If we go 10 units to the right, we get to x = 35: we can’t be here, at a distance equal to 10, but we could be the right of x = 35, at a distance of more than 10. Thus, the solution includes the pair of regions x < 15 and 35 < x.

Notice that x = 25 is the point of symmetry of this diagram, since everything is about distance from that point.
Summary of absolute value inequalities
The perspective above may give you some insight into this problem. If you had any “aha” moments reading this, then you might want to give the practice problems another try before looking at the solutions below. The solutions may afford you a few more insights into problem solving.

Practice Problem Explanations
1) Step one: find the midpoint of the region. The midpoint, halfway between and 20 and 90, is 55. In other words, 20 and 90 have the same distance from 55, a distance of 35. These endpoints are not included, but the region includes all the points that have a distance from from x = 55 that is less than 35. Translating that into math, we get the following:
|x – 55| < 35
Answer = (E)
2) Some folks might think this involves a sophisticated calculation, but much of this can be done with simple spatial analysis. Look at the second inequality, the more complicated one: |x – 8| > |x + 4|. All this says is that we are looking for points such that the distance to x = 8 is greater than the distance from x = –4; in other words, we want all the points that are closer to x = –4 and farther from x = 8.
The midpoint between x = –4 and x = 8 is the point x = 2. This point is not included because it’s equidistant from both points, but everything to the left of this point on the number line is closer to x = –4 than it is to x = 8. That entire complicated inequality simplifies to x < 2.
Combine that with the first inequality, |x| < 20, which in the negative realm means that x must be greater than –20. Thus, the allowed region is –20 < x < 2.
Answer = (B)
3) For this one, we need to be clever in a few ways. First of all, the expression inside the absolute value on the left is of the form [a square] + [a positive number]. Anything squared is either zero or positive, because something squared can never be negative. When we add a positive number, we are guaranteed that it is always positive. Thus, the absolute values around it are entirely superfluous, because it’s always positive anyway. We can remove those absolute value signs on the left with changing the mathematical meaning of the statement one bit.

The other expression, (x – 7), could be positive or negative, depending on the value of x, so it may equal +(x – 7) or it may equal –(x – 7). We have to investigate either case.
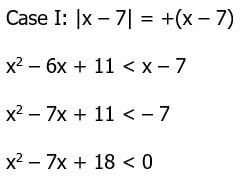
Think about the graph of a parabola.
![]()
This is an upward opening parabola, one that goes up on both sides. As you may know,
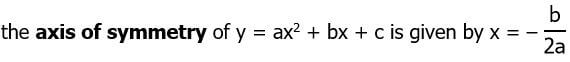
Furthermore, the vertex of the parabola is on this axis of symmetry. For this particular parabola, we get x = –(–7)/(2*1) = 7/2 as the axis of symmetry. Plug this value in to find the height of the vertex.
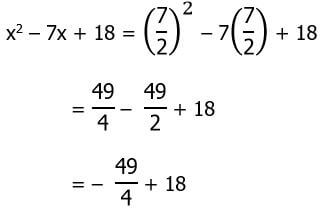
We don’t have to solve that last expression. The fraction 49/4 is between 12 and 13, so when this is subtracted from 18, we get something between 5 and 6. In other words, the vertex of this parabola starts above the x-axis and continues up. In other words, it is never negative, never less than zero. This means that the Case I inequality has no solutions.
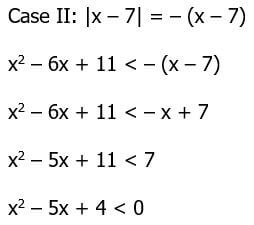
We can solve the equation to find the boundary points. We will have to factor the quadratic.
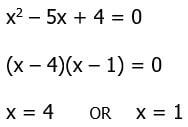
Think about the graph of this parabola.
![]()
This is also an upward opening parabola, also one that goes up on both sides. It equals zero at x = 1 and x = 4, so it must have its vertex between them, and it must be negative between those two points and positive to the left of x = 1 and to the right of x = 4. Thus, the solution of the Case II inequality is 1 < x < 4.
Since Case I had no solution, the Case II solution is the whole shebang.
Answer = (A)




Leave a Reply