Let’s recap where we left off yesterday. We were working with this diagram:
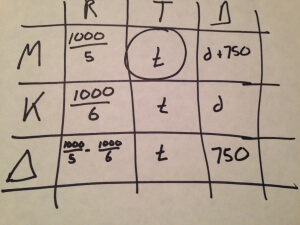
We wanted to solve for Mary’s time, t.
In every row the relationship among rate, time, and distance is the same: RT=D. In this diagram the bottom row looks the most promising, since it alone contains only the variable for which we’re solving. (Why mess around with d if we don’t need to?) So let’s look at the equation implicit in that bottom row:
Cross-multiplying to get the difference between those fractions yields:
or:
Could I have made the table simpler?
Yes. I wanted to show an efficient use of the table, but I didn’t want to insist on the optimal use.
You could, for instance, have represented Mary’s rate as 200 rather than as 1000/5, and Kate’s rate as 500/3 rather than as 1000/6. Doing that in the diagram or simplifying the moment you’d pull the equation out of the diagram would have yielded ![]() instead of
instead of ![]() That would have allowed you to multiply through by 3 rather than to cross-multiply:
That would have allowed you to multiply through by 3 rather than to cross-multiply:
That definitely saves some time and effort, but if our first, efficient-but-not-optimal use of the table comes more easily, that’s OK. Sometimes there’s a little trade-off between the ease of translation (English-into-algebra) and the ease of solution (algebraic manipulation).
By the way, I wouldn’t take it a step further and represent Kate’s rate as . Mixed numbers are usually more difficult to clear than are improper fractions.
But some uses of the RTD table are really inefficient!
For instance, many people build RTD tables with no bottom row for the sum or the difference of the rates and distances. This is just inviting complexity and computational error. Such a table often yields a system of two equations and two variables rather than a single equation with a single variable.
Consider what our table would have looked like with no bottom roappw:
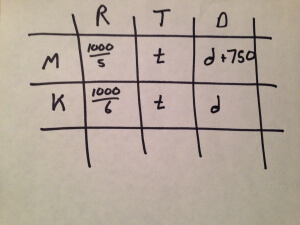
This would have yielded a system of equations:
If you distribute those fractions right away you’re in for a lot of work. It might occur to you to instead isolate t in each equation, then to solve for d, and finally to solve for t. It turns out that that, too, is a lot of work:
But 3750 isn’t one of our answers! That’s because we’re solving for t rather than for d. We have to return to one of our equations that related t to d, substitute 3750 for d, and solve for t:
Bottom-line? Always include an extra row for simultaneous-movement problems. You won’t need to use it every time, but it will you save you a lot of trouble when you do need it.
Hey, I think that I could answer this problem without the table!
Well, then you probably could.
You might remember this formula from my earlier post on the RTD table: (combined rate)(time)=(combined distance). We used that for travelers moving simultaneously in opposite directions.
Here’s a similar, and similarly simple, formula for travelers moving simultaneously in the same direction: (difference in rates)(time)=(difference in distances).* Applying that formula to this problem directly yields our equation:
![]()
You’ve still got to do the math, of course.
*In fact, some people point out that the second formula is just a special case of the first, since subtraction is one way to combine values. I find that confusing, since for non-mathematicians like us “combined” usually means “added.”
Next time, a really hard rate problem.
Just in case you’ve patiently read these posts on the RTD table and you still haven’t seen a problem that you couldn’t translate directly from English to Algebra, my next post will feature a more complicated rate problem.

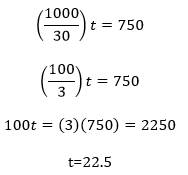

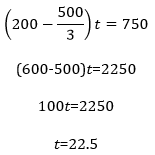
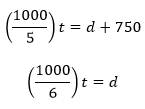
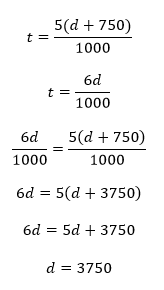
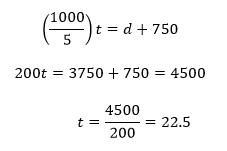




Leave a Reply