Understand the properties of the GMAT Quantitative section’s two favorite triangles!
The two special triangles are right triangles with special angles and side. Like all right triangles, they satisfy the Pythagorean Theorem. These two triangles are “special” because, with just a couple pieces of information, we can figure out all their properties. The GMAT-writers love this about these two triangles, so these special triangles are all over the place on the GMAT Quantitative Section. In what follows, do your best to understand the argument: remembering what you understand is far more effective than simple memorizing.
The 45-45-90 Triangle
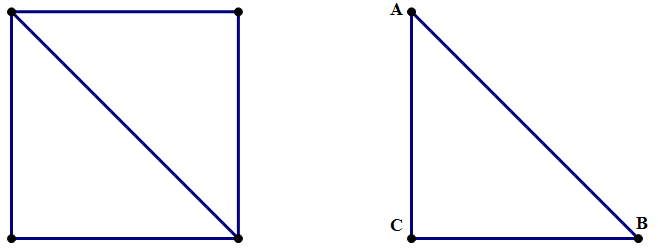
Let’s start with the square, that magically symmetrical shape. Assume the square has a side of 1. Cut the square in half along a diagonal, and look at the triangle that results.
We know ∠C = 90º, because it was an angle from the square. We know AC = BC = 1, which means the triangle is isosceles, so ∠A = ∠B = 45º. Let’s call hypotenuse AB = x. By the Pythagorean Theorem,
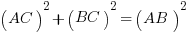
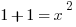
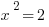
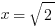
The sides have the ratios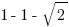 
. We can scale this up simply by multiplying all three of those by any number we like: 
.
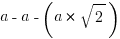So, the three “names” for this triangle (which are useful to remember, because they summarize all its properties) are
1) The Isosceles Right Triangle
2) The 45-45-90 Triangle
3) The 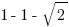Triangle
The 30-60-90 Triangle
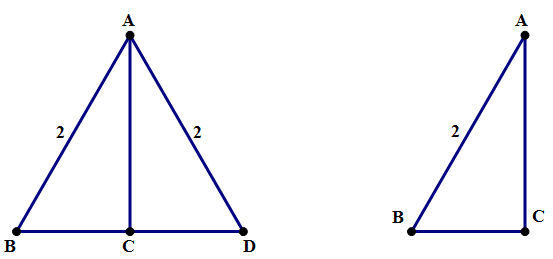
Let’s start with an equilateral triangle, another magically symmetrical shape. Of course, by itself, the equilateral triangle is not a right triangle, but we can cut it in half and get a right triangle. Let’s assume ABD is an equilateral triangle with each side = 2. We draw a perpendicular line from A down to BD, which intersects at point C. Because of the highly symmetrical properties of the equilateral triangle, the segment AC (a) forms a right angle at the base, (b) bisects the angle at A, and (c) bisects the base BD.
So, in the triangle ABC, we know ∠B = 60º, because that’s the old angle of the original equilateral triangle. We know ∠C = 90º, because AC is perpendicular to the base. We know ∠A = 30º, because AC bisects the original 60º angle at A in the equilateral triangle. Thus, the angles are 30-60-90. We know AB = 2, because that’s a side from the original equilateral triangle. We know BC = 1, because AC bisects the base BD. Call AC = x: we can find it from the Pythagorean Theorem.
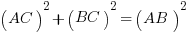
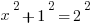
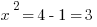
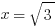
The sides are in the ratio of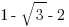 
. This can be scaled up by multiplying by any number, which gives the general form: 
.
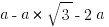So, the three “names” for this triangle (which are useful to remember, because they summarize all its properties) are
1) The Half-Equilateral Triangle
2) The 30-60-90 Triangle
3) The 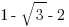Triangle
Summary
Math is not a spectator sport. Now that you have seen these arguments, see if you can re-create the entire argument for the properties without looking at this post. If you can remember, or even half remember, the entire argument, that will be enormously beneficial in remembering the properties themselves.
Here are some free practice questions:
1) http://gmat.magoosh.com/questions/1017
2) http://gmat.magoosh.com/questions/1016
Leave a Reply