Learn this powerful method for unlocking devilishly complicated problems about sets.
Practice questions
First, try these challenging 700-level practice questions.
1) At Veridux Corporation, there are 250 employees. Of these, 90 are female, and the rest are males. There are a total of 40 managers, and the rest of the employees are associates. If there are a total of 135 male associates, how many female managers are there?
A. 15
B. 20
C. 25
D. 30
E. 35
2) In the county of Veenapaniville, there are a total of 50 high schools, of three kinds: 25 public schools, 16 parochial schools, and 9 private independent schools. These 50 schools are divided between three districts: A, B, and C. District A has 18 high schools total. District B has 17 high schools total, and only two of those are private independent schools. If District C has an equal number of each of the three kinds of schools, how many private independent schools are there in District A?
A. 2
B. 3
C. 4
D. 5
E. 6
This kind of question
It would not be surprising if you found one or both of those questions totally bewildering. Without the right method, this type of question can be a nightmare.
First of all, let’s be clear about what we mean by “this type of question.” These are set questions in which each element, each member, is classified according to two different variables, and each one of those variables has two or more categories. For example, in question #1, the two variables are:
a) gender (male or female)
b) employee type (manager or associate)
Every one of those 250 employees is categorized both in terms of gender and in terms of employee type. That’s key: every member is categorized in two different ways. This type of question is screaming for a method of solution called the Double Matrix Method.
The Double Matrix Method: example #1
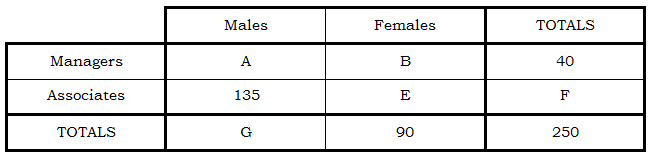
I will demonstrate the Double Matrix Method first by solving question #1, then question #2. In the Double Matrix Method, you make a sectioned box, a rectangle with subdivisions. The horizontal subdivisions will represent the categories of one variable, and the vertical subdivisions will represent the categories of the other variable. Here’s the set-up for question #1: I temporarily put letters in the boxes, to facilitate talking about those boxes.
A is number of male managers, B is the number of female managers, and A + B = C is the total number of managers. Similarly, D is the number male associates, and A + D = G is the total number of males. In any row, you can add across the first two boxes and the sum will be the box on the right. In any column, you can add the top two boxes, and the sum will be the bottom box. The final number, I, is the “grand total”, the total number of employees in the whole problem, which obvious has to equal the sum of males + females, as well as the sum of managers + associates.
Here’s that matrix again with the numbers from the problem filled in — just the numbers stated in black-and-white in the problem.
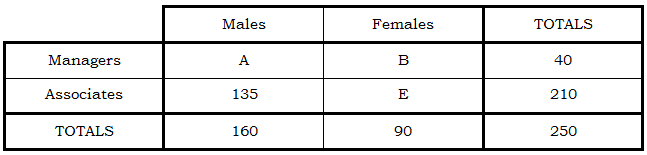
Well, first let’s take care of the “totals”. The numbers in the “totals” row must add up. If 90 are females, the other 250 – 90 = 160 must be males. Similarly, the numbers in the “totals” column must add up. If 40 are managers, then the other 250 – 40 = 210 must be associates.
Now, in the “associate” row, 135 + E = 210, which means E = 75 — the other 75 associates must be female.
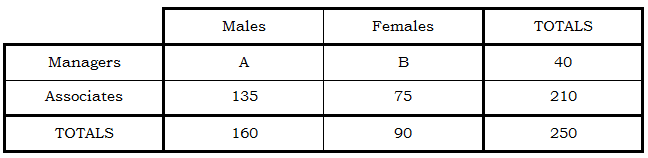
Now, to find B, which is what the question is asking, we need only look at the sum in the “female” column: B + 75 = 90, which means B = 15. There are fifteen female managers in this company. Thus, the answer = (A).
Instead of this route, once we found all the “totals” numbers, we could have used addition in the “male” column to find A = 25, then use addition across the “managers” to find B = 15 —- in fact, if you have a second route for finding the number, you should perform that too, to verify that you get the same number both ways.
The Double Matrix Method: example #2
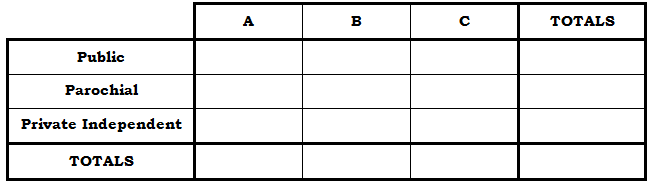
Question #2 is very difficult: it’s debatable whether a set question this difficult even would appear on the GMAT. Nevertheless, the Double Matrix Method unlocks it easily. First of all, our matrix now has to have three categories for each variable.
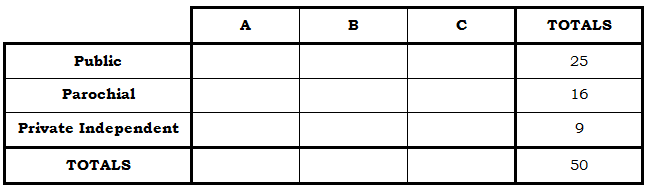
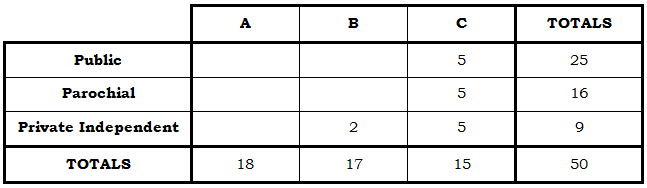
As before, in any row, the sum across the first three entries will equal the right-most entry in the “totals” column; and similarly, the sum down the top three entries in any column will equal the bottom entry in the “total” row; and, of course, all the totals, in either the “totals” row or the “totals” column, have to add up to the grand total in the lower right-hand box. Let’s start filling this in, following the information given in the question. “In the county of Veenapaniville, there are a total of 50 high schools, of three kinds: 25 public schools, 16 parochial schools, and 9 private independent schools.”
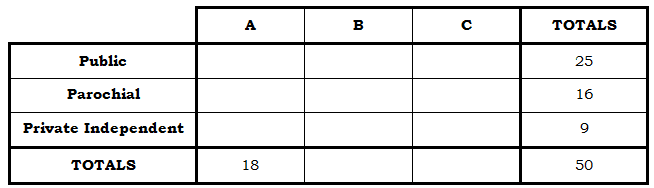
“District A has 18 high schools total.”
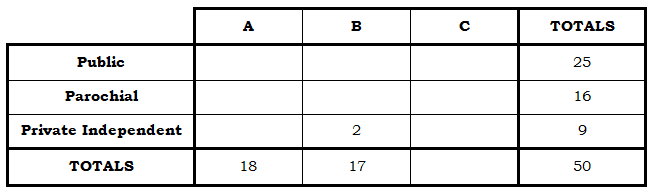
“District B has 17 high schools total, and only two of those are private independent schools.”
“District C has an equal number of each of the three kinds of schools.” Hmm. That’s not a simple number. Let’s put that on hold for a moment. So far, from the matrix it looks like we could figure out the missing number in the “totals” row. That number must be 15, because 18 + 17 + 15 = 50.
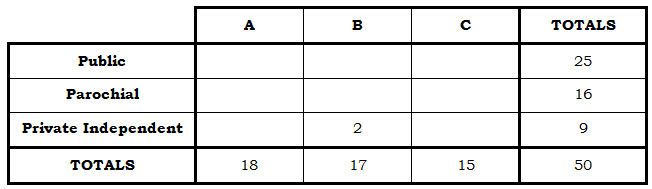
Now, go back to that last fact: “District C has an equal number of each of the three kinds of schools.” Now that makes sense. District C has 15 schools, so it must have 5 of each kind:
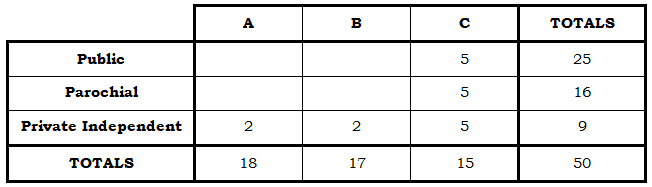
The question is asking: “how many private independent schools are there in District A?” Well, now that’s just a matter of adding across the “private independent” row. We know 2 + 2 + 5 = 9, so the missing number must be 2.
There’s still a good deal of information we can’t figure out from the information given in the question, but we are able to answer the specific question asked here. There are 2 private independent schools in District A, so the answer = (A).
Notice, incidentally, if the question were framed differently, as a DS question, the Double Matrix method would allow us to see what questions we could and couldn’t answer based on the information given. In a DS question, one would have to write out one Double Matrix for Statement #1, and a whole new Double Matrix for Statement #2. Trying to save time by cramming all the information from both statements into a single matrix is an excellent way to make the classic mistake of conflating the information given in the two statements, one of the most common mistakes on Data Sufficiency.
Practice question
Here’s another very challenging question that you should be able to unlock with the help of the Double Matrix Method.
3) http://gmat.magoosh.com/questions/11







Leave a Reply