The 45º angle
Fact: All lines with slopes of 1 make 45º angles with both the x- and y-axes.
Conversely, if a line makes a 45º angles with either the x- of y-axes, you know immediately its slope must be 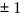 . This first fact is true, not only for y = x and y = –x, for all lines of the form y = mx + b in which m equals either 1 or –1. If the slope is anything other than
. This first fact is true, not only for y = x and y = –x, for all lines of the form y = mx + b in which m equals either 1 or –1. If the slope is anything other than 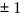 , you would need trigonometry to figure out the angles, and that’s beyond the scope of GMAT math. The GMAT could expect you to know this one fact about these special lines, especially on Data Sufficiency.
, you would need trigonometry to figure out the angles, and that’s beyond the scope of GMAT math. The GMAT could expect you to know this one fact about these special lines, especially on Data Sufficiency.
As a Mirror
Fact: Suppose we treat the line y = x as a mirror line. If you take any point (a, b) in the coordinate plane, and reflect it over the line y = x, the result is (b, a). It reverses the x- and y-coordinates!
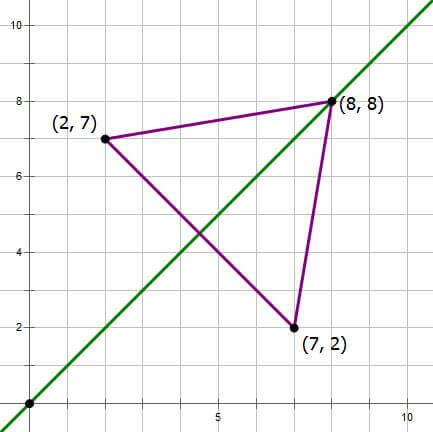
The corollary of this is that if we compare any two points with reversed coordinates, say (2, 7) and (7, 2), we automatically know that each is the image of the other by reflection over the line y = x. Add now the geometry fact that a mirror line is the set of all points equidistant from the original point and its image. This means that the midpoint of the segment connect (2, 7) and (7, 2) must lie on the line y = x. In fact, any point on the line y = x will be equidistant from both (2, 7) and (7, 2). Without doing a single calculation, we know, for example, that the triangle formed by, say, (2, 7) and (7, 2) and (8, 8 ) must be an isosceles triangle. (See the diagram below.)
When we reflex over the line y = –x, the coordinate are reversed and made their opposite sign: e.g. (2, 7) reflect to (–7, –2), and (–5, 3) reflects to (–3, 5). The other conclusions, about equidistance, remain the same.
As a Boundary
Fact: Any point (x, y) in the coordinate plane that is above the line y = x has the property that y > x. Any point (x, y) in the coordinate plane that is below the line y = x has the property that y < x.
Can you sense the veritable cornucopia of Data Sufficiency questions that could arise from this fact? If you every see a question about the coordinate plane asking whether y > x or y < x, chances are very good that the line y = x is hidden somewhere in the question.
Practice Questions
1) Is the slope of Line 1 positive?
Statement #1: The angle between Line 1 and Line 2 is 40º.
Statement #2: Line 2 has a slope of 1.
(A) Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
(B) Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
(C) Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
(D) Each statement alone is sufficient to answer the question
(E) Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
2) Point (P, Q) is in the coordinate plane. Is P > Q?
Statement #1: P is positive.
Statement #2: Point (P, Q) above is on the line y = x + 1
(A) Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
(B) Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
(C) Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
(D) Each statement alone is sufficient to answer the question.
(E) Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
3) A circle has a center at P = (–4, 4) and passes through the point (2, 3). Through which of the following must the circle also pass?
(A) (1, 1)
(B) (1, 7)
(C) (–1, 9)
(D) (–3, –2)
(E) (–9, 1)
Practice Questions Explanations
1) A straightforward prompt.
Statement #1 is intriguing: it gives us a specific angle measure. This is tantalizing, but unfortunately, it is only the angle between Line 1 and Line 2, and that angle could be oriented in any direction. Therefore, we can draw no conclusion about the prompt from this statement alone. Statement #1, by itself, is insufficient.
Statement #2 is also tantalizing, because it’s numerically specific. But, unfortunately, this tells us a lot about Line 2 and zilch about Line one, so this statement is, by itself, is also insufficient.
Now, combine the statements. From statement #2, we know Line 2 has a slope of 1, which means the angle between Line 2 and the positive x-axis is 45º. We know, from statement #1, that Line #1 is 40º away from Line 2. We don’t know which way, above or below Line 2. If Line 1 is steeper than Line 2, it makes an angle of 45º + 40º = 85º with the positive x-axis. If Line 1 is less steep than Line 2, it makes an angle of 45º – 40º = 5º with the positive x-axis. Either way, its angle above the positive x-axis is between 0º and 90º, which means it has a positive slope. The combined statements allow us to give a definitive answer to the prompt question. Answer = C.
2) We see the x > y type question in the prompt, which makes us suspect that the line y = x will play an important part at some point.
Statement #1 just tells us P is positive, nothing else. The point (P, Q) = (4, 2) has the property that P > Q, but the point (P, Q) = (4, 5) has the property that P < Q. Clearly, just knowing P is positive does nothing to help us figure out whether P > Q. Statement #1, by itself, is wildly insufficient.
Statement #2 is intriguing. It discusses not the line y = x but the line y = x + 1. What is the relationship of those two lines? First of all, they are parallel: they have the same slope. The line y = x has a y-intercept of zero (it goes through the origin), while the line y = x + 1 has a y-intercept of 1. This means: any point on the line y = x + 1 must be above the line y = x. If (P, Q) is on y = x + 1, then it is above y = x, which automatically means Q > P. We can give a definite “no” answer to the question. By itself, Statement #2 is sufficient. Answer = B.
3) For this problem, there’s a long tedious way to slog through the problem, and there’s a slick elegant method that gets to the answer in a lightning fast manner.
The long slogging approach — first, calculate the distance from (–4, 4) to (2, 3). As it happens, that distance, the radius, equals 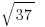 . Then, we have to calculate the distance from (–4, 4) to each of the five answer choices, and find which one has also has a distance of
. Then, we have to calculate the distance from (–4, 4) to each of the five answer choices, and find which one has also has a distance of 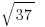 —- all without a calculator. 🙁
—- all without a calculator. 🙁
The slick elegant approach is as follows. The point (–4, 4) is on the line y = –x, so it is equidistant from any point and that point’s reflection over the line y = –x. The reflection of (2, 3) over the line y = –x is (–3, –2). Since (–3, –2) is the same distance from (–4, 4) as is (2, 3), it must also be on the circle. Answer = D.





Leave a Reply