This post was updated in 2024 for the new GMAT.
Here are twelve challenging problems related to the topic of exponents & roots. Remember, no calculator.
(A) 17
(B) 19
(C) 21
(D) 23
(E) 27
4) Rank the following quantities in order, from smallest to biggest.
(A) I, II, III
(B) I, III, II
(C) II, I, III
(D) III, I, II
(E) III, II, I
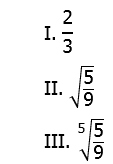
5) Rank the following quantities in order, from smallest to biggest.
(A) I, II, III
(B) I, III, II
(C) II, I, III
(D) III, I, II
(E) III, II, I
(A) 96
(B) 120
(C) 144
(D) 192
(E) 288
(A) 4,000
(B) 8,000
(C) 16,000
(D) 25,000
(E) 125,000
8) Rank the following quantities in order, from smallest to biggest.
(A) I, II, III
(B) I, III, II
(C) II, I, III
(D) II, III, I
(E) III, II, I
(A) 1/5
(B) 2/13
(C) 2/15
(D) 5/3
(E) 15/2
Exponents and roots
For a review of some of the basics, see these blogs:
1) Exponent Properties on the GMAT
2) Adding and Subtracting Powers on the GMAT
3) Roots
5) Practice Problems on Powers and Roots
If reading any of those blogs gives you some insight, you might want to give the problems a second look before proceeding the solutions below.
Practice problems explanations
1) For this one, we can eliminate choices (A) & (B) because they make ghastly exponent mistakes. For the other three, we would have to add and subtract the powers of each, to see which work, trying each by trial and error.
Instead, here’s an elegant solution. Notice that the product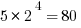 
. So, this is 80 times a power of 3. Now, notice that 80 = 81 – 1. In other words, we can easily express the factor 80 as the difference of two powers of 3. Thus.
Answer = (E).
2) We have to begin with some clever noticing. Notice, first of all, that 409 = 400 + 9. This suggests a difference of two squares factoring pattern. Notice that the numerator can be expressed as 159,919 = 160,000 – 81. That’s a difference of two squares that can be factored!
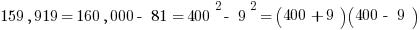
The first parenthesis produces 409. The second parenthesis contains another difference of two squares:
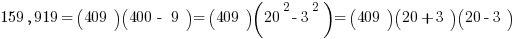
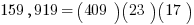
Therefore, if we divide by sides by (409)(17), we get that the fraction equals 23.
Answer = (D).
3) Well, we know that 15 = 3*5, and we have the exponent that gives a 5, but how do we get an exponent that gets a 3? Well, of course [pmath]6^1 = 6[/pamth], and therefore
and therefore
Answer = (E).
4) First of all, the fact that 120 is a multiple of 30 draws our attention to that comparison. The ratio 120:30 = 4:1, so we just would have to compare those powers of 2 and 17.
So, III is bigger than I. Now, notice that the exponents of I and II are also in a convenient ratio — 120:72 = 5:3. We can use those exponents on 2 and 3.
Therefore, II is smaller than I. From smallest to biggest: II, I, III.
Answer = (C).
5) First of all, clearly
So, II is bigger than I. Now, what about III? When we take higher order roots, the values move closer to one. If the number starts larger than one, then higher and higher roots make it smaller, closer to one. If the number starts between 0 and 1, then higher and higher roots make it larger, closer to one. Therefore, III is larger than II. From smallest to biggest, I, II, III.
Answer = (A).
6) First of all, the mistake: we CANNOT add through
That incorrect thinking would lead to the trap answer of (B). Instead, we have to simplify each square root on the left.
Answer = (D).
7) This one becomes clearer if we change the roots to fractional exponents.
Answer = (A).
8) The exponent of 3, which is 42, is close to 40. If 2 and 3 had exponents of 60 and 40, respectively, those would be in a ratio easy to reduce — 60:40 = 3:2. Clearly
Raise both sides of that inequality to the power of 20.
Therefore, III is bigger than I.
Now, let’s think about II. The square root of 2 is 2 to the power of 1/2, so 2 times the square root of two, the contents of the parentheses, would be 2 to the power of 1.5. Multiply the exponents: 1.5*35 = 35 + 17.5 = 52.5 — that would be the resultant exponent of 2. Clearly, this is a lower power of 2 than given in statement I. So, II is less than I.
From smallest to biggest is II, I, III.
Answer = (C).
9) An increase of 50% corresponds to a multiplier of 1.5, so the above information can be written as
To get all the K’s on one side, we will divide by the power on the left, K to the power of 5/4. This will mean we have to subtract the exponents. What do we get when we subtract 5/4 from 3/2?
Thus, after the division, we have:
Now, raise both sides to the fourth power to solve for K:
Answer = (E).
10) First, we have to express 0.15 as a fraction:
Also, 16 is 2 to the power of 4, so the equation with b tells us:
Bases are the same, so we can equate the exponents.
Answer = (E).
11) As is usual, all the answer choices have been rationalized, so we have to rationalize the denominator of the prompt fraction. This means multiplying by the conjugate over itself: that would be 7 minus 3 times the square root of 5.
In the denominator, we use the difference of two squares pattern. In the numerator, we simply FOIL.
Answer = (D).
BTW, you don’t need to know this for the GMAT, but this OA answer is the reciprocal of the Golden Ratio, and answer choice (E) equals the Golden Ratio.
12) We need to express each side as a power of 5. We will use fractional exponents for the roots.
Equate the exponents.
Multiply both sides by 6 to clear the fractions.
Answer = (B).
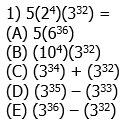
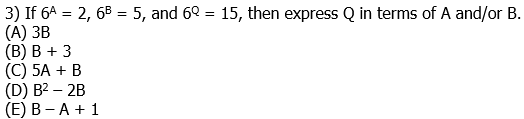
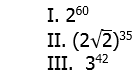
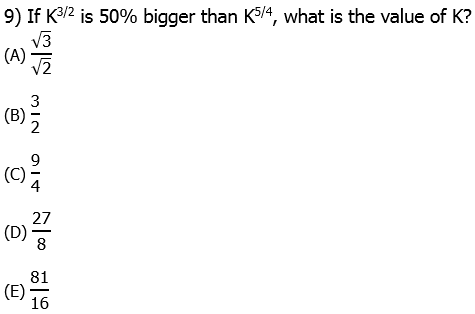
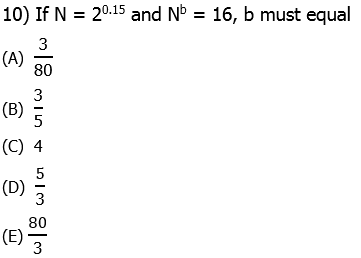
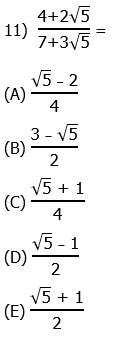
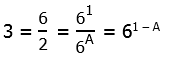
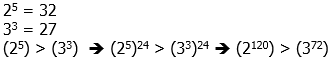
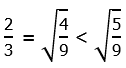
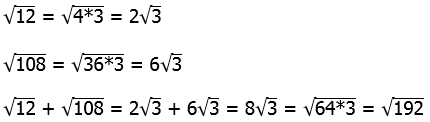
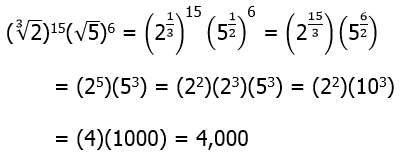
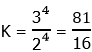
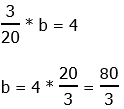
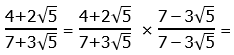
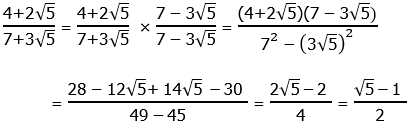
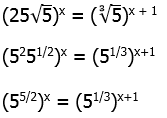
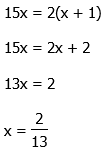
Leave a Reply