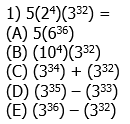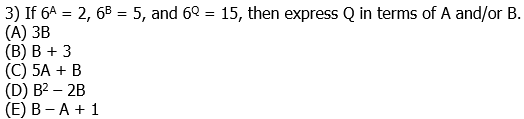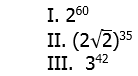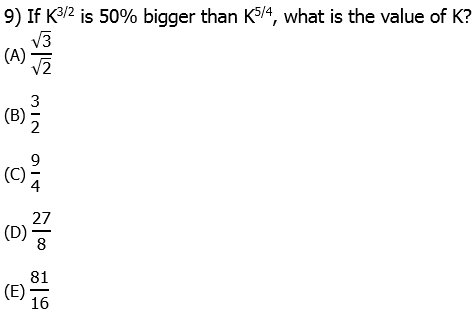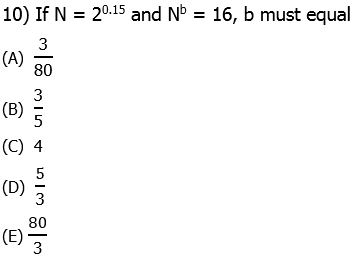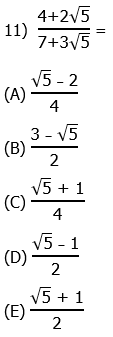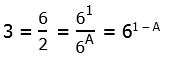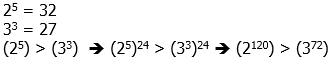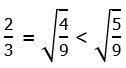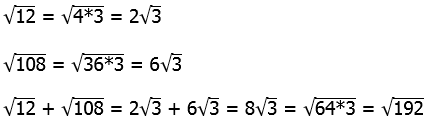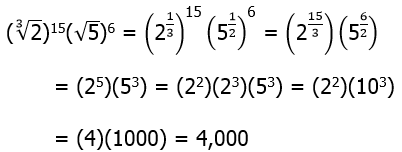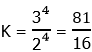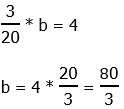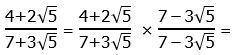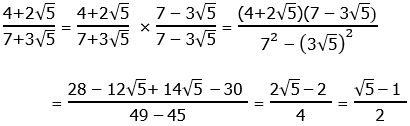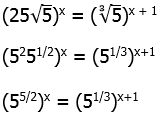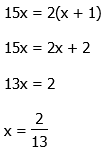Here are twelve challenging problems related to the topic of exponents & roots. Remember, no calculator.
(A) 17
(B) 19
(C) 21
(D) 23
(E) 27
4) Rank the following quantities in order, from smallest to biggest.
(A) I, II, III
(B) I, III, II
(C) II, I, III
(D) III, I, II
(E) III, II, I
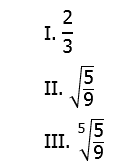
5) Rank the following quantities in order, from smallest to biggest.
(A) I, II, III
(B) I, III, II
(C) II, I, III
(D) III, I, II
(E) III, II, I
(A) 96
(B) 120
(C) 144
(D) 192
(E) 288
(A) 4,000
(B) 8,000
(C) 16,000
(D) 25,000
(E) 125,000
8) Rank the following quantities in order, from smallest to biggest.
(A) I, II, III
(B) I, III, II
(C) II, I, III
(D) II, III, I
(E) III, II, I
(A) 1/5
(B) 2/13
(C) 2/15
(D) 5/3
(E) 15/2
Exponents and roots
For a review of some of the basics, see these blogs:
1) Exponent Properties on the GMAT
2) Adding and Subtracting Powers on the GMAT
3) Roots
5) Practice Problems on Powers and Roots
If reading any of those blogs gives you some insight, you might want to give the problems a second look before proceeding the solutions below.
Practice problems explanations
1) For this one, we can eliminate choices (A) & (B) because they make ghastly exponent mistakes. For the other three, we would have to add and subtract the powers of each, to see which work, trying each by trial and error.
Instead, here’s an elegant solution. Notice that the product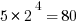 
. So, this is 80 times a power of 3. Now, notice that 80 = 81 – 1. In other words, we can easily express the factor 80 as the difference of two powers of 3. Thus.
Answer = (E).
2) We have to begin with some clever noticing. Notice, first of all, that 409 = 400 + 9. This suggests a difference of two squares factoring pattern. Notice that the numerator can be expressed as 159,919 = 160,000 – 81. That’s a difference of two squares that can be factored!
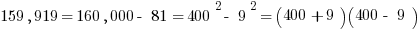
The first parenthesis produces 409. The second parenthesis contains another difference of two squares:
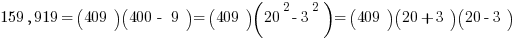
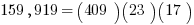
Therefore, if we divide by sides by (409)(17), we get that the fraction equals 23.
Answer = (D).
3) Well, we know that 15 = 3*5, and we have the exponent that gives a 5, but how do we get an exponent that gets a 3? Well, of course [pmath]6^1 = 6[/pamth], and therefore
and therefore
Answer = (E).
4) First of all, the fact that 120 is a multiple of 30 draws our attention to that comparison. The ratio 120:30 = 4:1, so we just would have to compare those powers of 2 and 17.
So, III is bigger than I. Now, notice that the exponents of I and II are also in a convenient ratio — 120:72 = 5:3. We can use those exponents on 2 and 3.
Therefore, II is smaller than I. From smallest to biggest: II, I, III.
Answer = (C).
5) First of all, clearly
So, II is bigger than I. Now, what about III? When we take higher order roots, the values move closer to one. If the number starts larger than one, then higher and higher roots make it smaller, closer to one. If the number starts between 0 and 1, then higher and higher roots make it larger, closer to one. Therefore, III is larger than II. From smallest to biggest, I, II, III.
Answer = (A).
6) First of all, the mistake: we CANNOT add through
That incorrect thinking would lead to the trap answer of (B). Instead, we have to simplify each square root on the left.
Answer = (D).
7) This one becomes clearer if we change the roots to fractional exponents.
Answer = (A).
8) The exponent of 3, which is 42, is close to 40. If 2 and 3 had exponents of 60 and 40, respectively, those would be in a ratio easy to reduce — 60:40 = 3:2. Clearly
Raise both sides of that inequality to the power of 20.
Therefore, III is bigger than I.
Now, let’s think about II. The square root of 2 is 2 to the power of 1/2, so 2 times the square root of two, the contents of the parentheses, would be 2 to the power of 1.5. Multiply the exponents: 1.5*35 = 35 + 17.5 = 52.5 — that would be the resultant exponent of 2. Clearly, this is a lower power of 2 than given in statement I. So, II is less than I.
From smallest to biggest is II, I, III.
Answer = (C).
9) An increase of 50% corresponds to a multiplier of 1.5, so the above information can be written as
To get all the K’s on one side, we will divide by the power on the left, K to the power of 5/4. This will mean we have to subtract the exponents. What do we get when we subtract 5/4 from 3/2?
Thus, after the division, we have:
Now, raise both sides to the fourth power to solve for K:
Answer = (E).
10) First, we have to express 0.15 as a fraction:
Also, 16 is 2 to the power of 4, so the equation with b tells us:
Bases are the same, so we can equate the exponents.
Answer = (E).
11) As is usual, all the answer choices have been rationalized, so we have to rationalize the denominator of the prompt fraction. This means multiplying by the conjugate over itself: that would be 7 minus 3 times the square root of 5.
In the denominator, we use the difference of two squares pattern. In the numerator, we simply FOIL.
Answer = (D).
BTW, you don’t need to know this for the GMAT, but this OA answer is the reciprocal of the Golden Ratio, and answer choice (E) equals the Golden Ratio.
12) We need to express each side as a power of 5. We will use fractional exponents for the roots.
Equate the exponents.
Multiply both sides by 6 to clear the fractions.
Answer = (B).
Hey are these sub 500 or 600 to 700 level?
Hi Varun,
These are difficult questions, but here at Magoosh we don’t label questions based on GMAT score. You can see more here: https://magoosh.com/gmat/is-this-a-700-level-gmat-question/
For number two, I used an approach that got me to the right answer quickly but I am not sure if it is foolproof. Can anyone check it over and tell me if this method works for a plethora of problems or not? Thanks.
When looking at the problem, I noticed that there are answers that all have different ones place digits except a pair of answers (A and E), thus if I could find out the answer in just the ones digit, I could either reduce my guessing between two choice or the right choice.
In the denominator, the ones digit will be a 3 (409 * 17 = XXX,XX3). Numerator / Denominator is XXX,XX9 / XXX,XX3, this results in the answer having a 3 in its ones place.
Is there a typo in #12? How do we jump from step 1 of the explanation to step 2?
Hi Nicole,
The key here is to see that if we can make the base of the exponents equal, then the expressions in the exponents must also be equal. So if we can make the base of both sides equal to 5, then we can solve x by setting the exponents equal to each other. The first part of this explanation is focused on making the base become 5, and then we ignore the base entirely and just set the exponents equal to each other. I hope this helps!
Hi! Firstly, thanks very much for these problems! Secondly, I have a question about no. 5. The problem asks for ordering of the options from smallest to biggest. Making the denominator the same for each fraction (3) gives the following numerators for options I, II and III respectively. 2, root5, 5root5. 5root5<2<root5. Therefore, is the correct order from smallest to biggest not III, I, II?
Hi John,
You can create like denominators for easier comparison of this question, but I think you made a slight mistake with your math 🙂
If we simplify √9 to 3 in the denominator of II, then we have the following three numbers: 2/3, √5/3 and (5√5)/(5√9). Here, 5 denotes the fifth root–sorry there’s no easy way to put those symbols! Since we don’t have any common multipliers, we the only option for the common denominator is 3 multiplied by the fifth root of 9: 3*(5√9).
In order to create common denominators, we have to multiply both the numerator and denominator by the number that will create the common denominator. So we multiply the numerators and denominators of I and II by (5√9) and those of III by 3. When we multiply the we would be left with the following three fractions:
I. (2(5√9))/(3*(5√9))
II. (√5(5√9))/(3*(5√9))
III. (3(5√9))/(3*(5√9)).
Since we have created like denominators and have the fifth root of 9 in each numerator, we are left to compare 2, √5 and 3 from the numerators. Since √5 is between 2 and 3, we see that the ascending order of these fractions is still A. I, II, III.
I hope that helps, and that you were able to follow the strange symbols here 🙂
can u guyz please tell me, what’s the name of the math topic in which we discuss these type of tricky exponent questions. I want to research on this. Please.
Hi Ahmad! To solve these questions, it’s key to be comfortable with the Laws of Exponents in addition to other concepts referenced in the “Practice problems explanations” section of the post 🙂
For number 2, I feel like most people wouldn’t “cleverly notice” that.
An interesting alternative is as follows:
Divide 159,919 by 17 (just some simple long division) = 9,407
Round 9407 to 9400
and Round 409 to 400
9400/400=23.5
The answers are far enough apart to realize that some rounding is allowed.
Magoosh’s explanation is very eloquent, but I know I would not have noticed it. This just may be another approach for anyone who is confused!
Hi Mike,
Would you say these types of problems are highly likely on the exam?
Thanks for your help!
Sneha
Good set of problems, good solutions. Thank you soo much for sharing them with us
Thanks, Aniket!