Advanced (Non-Calculator!) Factoring on the GMAT

June 5, 2012

Fact: On the GMAT Quantitative Section, you cannot use a calculator.

Therefore, if you are aiming to tackle even the 700-800 questions on the Q section, you need to have some crafty mental math tricks up your sleeve. One of the most powerful involves the clever use of a famous algebra formula: the difference of two squares formula. See this post for uses of that formula in general problem solving. Here we will focus on factoring.

Factoring Big Numbers

In general, factoring a big number can be time-consuming without a calculator. The GMAT might ask a question in which you need to know the factors, or the prime factorization, of a large number. See this post for more on prime factorizations.
First of all, notice how easy it is to square the multiples of 10. If you can square the numbers from 1 to 10, you can square the multiples of 10 from 10 to 100.

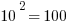
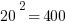
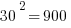
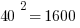
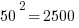
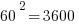
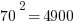
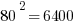
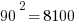
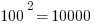
Those should all be recognizable as nice round perfect squares.
Now, suppose you are in a situation in which you have to factor, say, 1591, or 3551, or 8099. Notice, all of those are a perfect square less than one of these multiples of ten squared.

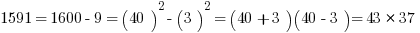
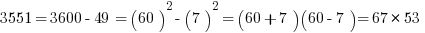
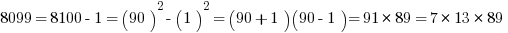
In general, the GMAT is not going to put you in a situation in which you have to find the prime factorization of a general four digit number. If this situation does arise, you can bet there’s an enormously simplifying trick available, and factoring via the difference of two squares is an awfully likely candidate for that trick.

Factoring Decimals

Just as the difference of two square can simplify factoring big numbers, it can also simplify factoring decimals. To demonstrate this, I am going to show the solution to a flamboyantly recondite question from the OG13e, viz., PS #199 on p. 180.

199)
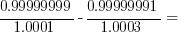
(A) 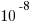10^-8
(B)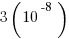
(C)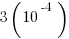
(D)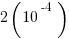
(E) 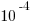10^-4

Notice that 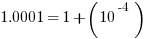, and .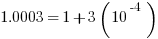

Now, notice that both numerators simplify via difference of two squares formula.

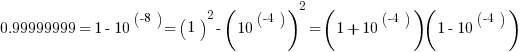
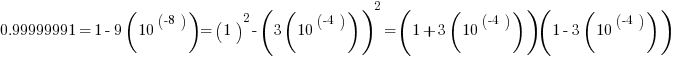
Thus, the two fractions become

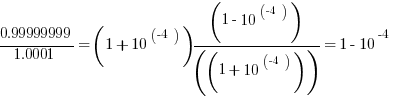
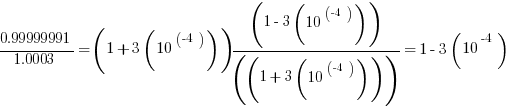
The difference:

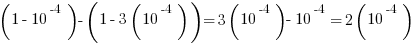
Answer = D

Here’s a related practice question.

http://gmat.magoosh.com/questions/129

Author

Mike MᶜGarry

Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as “member of the month” for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.

View all posts

Comments

4 responses to “Advanced (Non-Calculator!) Factoring on the GMAT”

Jodi

July 20, 2018

I don’t quite understand how you simplified that final step.

Reply
1. Magoosh Test Prep Expert
  
  July 22, 2018
  
  The final step takes advantage of a pattern in multiplication, a pattern that can work for any values. Here’s the pattern:
  
  (a-b) – (a-c) = c – b
  
  Like I said, this can work for any set of values. In the problem in his post, a = 1, b = 10 ^-4, and c = 3(10^-4). But let’s try this pattern with some simpler numbers to demonstrate how it works:
  
  (5-3) – (5-4) = 4-3 = 1 OR (5-3) – (5-4) = 2-1 = 1
  
  (1-9) – (1-1) = 1-9 = -8 OR (1-9) – (1-1) = -8-0 = -8
  
  Does that make sense? 🙂
  
  Reply
Faizan Qureshi

September 24, 2016

Do you believe that the GMAT will likely ask a question that will involve decimal difference of squares or will it be something “clean” like the practice problem that this blog is linked too? Thank you so much!

Reply
1. Magoosh Test Prep Expert
  
  September 25, 2016
  
  Hi Faizan,
  
  The GMAT problem will likely be clean. They understand that this is a timed exam and that you don’t have access to a calculator. Although they want to make the tough questions challenging, the questions are designed to be able to be completed quickly and cleanly. The difference of squares method is already challenging and difficult for most common test takers to notice immediately.
  
  Reply