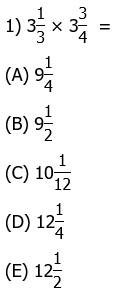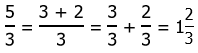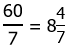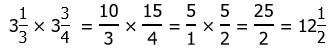This is the last of three part series:
a) Part One dealt with fraction addition and subtraction
b) Part Two dealt with fraction multiplication & division, including proportions
c) This part deals with improper fractions vs. mixed numerals
First, a practice question:
Solutions will appear at the end of this article.
Improper fractions
One of the first ways fractions are taught to kids is that the numerator is the “part” and the denominator is the “whole.” Thus, 2/7 of something means that the whole something has seven parts altogether and that we are currently considering two of these seven parts. This is a wonderful way to think about some fractions, but like many things taught in grade school, it’s not exactly the whole story. In fact, thinking about a fraction as an act of division, a perspective discussed in the first post, is something considerably more fundamental.
In particular, the part/whole analysis breaks down when the numerator is larger than the denominator. The fraction 5/3 is a totally legitimate fraction, but it doesn’t fit in the part/whole rubric: if the “whole” is 3, how could one have 5 “parts”? By contrast, in a real world scenario, one might have to divide, say, 5 large cookies equally among three children, so 5/3 would have a very real tangible meaning.
The fraction 5/3 is called an “improper fraction” because the numerator is larger than the denominator. That name is unfortunate and misleading, because mathematically, there is absolutely nothing “improper” about such a fraction. This is one legitimate way to represent the whole infinity of fractions that have a numerical value larger than one.
Mixed numerals
The other legitimate way to represent fractions greater one is mixed numerals. A mixed numeral has a whole number part, an integer, and then standing next to the whole number is a fraction less than one, a so-called “proper” fraction. Suppose we started with the improper fraction 5/3. We could express that 5 in the numerator as (3 + 2), and then we could split the fraction into two by this addition in the numerator:
Notice a very little appreciated fact: the mathematical relationship between the whole number piece and the fraction piece of a mixed numeral is addition!
Mixed numeral have a close kinship with what I would call “integer division,” the kind of division in which we get an integer quotient and a remainder. For example, if we divide 60 by 7, then 7 will go in to it 8 times with a remainder of 4. Similarly,
It’s important to be comfortable with changing improper fractions to mixed numerals, but it’s also important to be comfortable with changing mixed numerals to improper fractions.
Which is better?
It’s possible that you had some grade school teacher drum into your head that mixed numerals are always better than improper fractions. I would like to disabuse you of that particularly poisonous misconception.
Mixed numerals are much better than improper fractions if what you want to determine is location on the number line. While it’s possible that the Praxis Core Math Test could construct a question asking you where a particular value falls on the number line, but such a question would be rare.
For addition and subtraction, it’s a tie. It’s relatively inconvenient for either, and except for special cases, not much better for one than for the other.
The BIG difference is when you have to multiply or divide these fractions or raise them to powers. For these operations, mixed numbers are worse than useless! Those three operations are always much much easier to perform correctly when the numbers are in improper fraction form. In fact, in one problem type, the test will ask you to find the product or quotient of two mixed numerals, or ask you to raise a mixed numeral to a power, and all five answer choices will be in mixed numerals. The gigantic trap of such a question is to believe that one is supposed to do the calculation in mixed numeral form: 99% percent of the people who choose this route will get the problem incorrect, precisely because mixed numerals are worse than useless for such calculations. The way to approach such a problem is to convert any mixed numerals in the prompt to improper fractions, do the calculation, and then convert the answer back to mixed numeral form.
Summary
If reading this blog gave you any insights, you might want to go back to the practice problem at the top and re-think it before you look at the answers below. If you would like more information about fractions, consider signing up for Magoosh: we have a full library of math & writing & reading lessons to give you everything you need to meet the challenge of Praxis.
Practice Problem Explanation
1) As recommended in this blog, change both mixed numerals in the prompt to improper fractions, perform the calculations with any canceling, and then change back.
As always, cancel before you multiply! We can cancel the 3 with a factor of three in 15, and we can cancel a factor of 2 between the 4 and the 10.
Answer choice (E)