On the Praxis Core Mathematics Test, you will have to do problems with fractions. Ah, fractions! While mathematical folks love these little critters, I know that so many folks who are, shall we say, less-than-fond of mathematics would rather go through their whole life without ever thinking about fractions. Some math-phobic people might even think: OK, to avoid fractions entirely, I will just convert every fraction on the test to a decimal using the calculator. Unfortunately, that would be a particular bad strategy, for a myriad of reasons. You see, one reasons mathematicians like fractions is because they are often a huge shortcut. Fractions are also much more precise than decimals, and precision is the very soul of mathematics.
Even if you are the most ardent math-phobe, I hope to persuade you that you can handle the basics of fractions.
To start, here’s a practice question:
1) If (1/6) + x = (2/7), then which of the following is the value of x?
If this looks like pure Greek to you, take heart! Read this article first, then go back and give this question a try!
Fractions and mathematical thinking
Part of the problem with fractions is that folks learn the basics in grade school, long before the human brain is ready for abstraction. Folks learn mechanical procedures, which are the mental equivalent of muscle memory. The trouble is that five, ten, fifteen years after grade school, things get blurry. The problem with a rote mechanical procedure is that, you don’t have it done just right, you often have no way to correct it. Folks get confused with their blurry mechanical procedures, and they naively conclude, “I guess I just can’t do fractions!” It is unconscionable that middle school and high school math teachers allow so many intelligent students to draw such conclusions, but there it is.
In fact, as with everything in mathematics, you can’t just learn a procedure. You have to push yourself to understand the why-questions. In the best of all possible worlds, in high school, when you brain can handle abstraction, you should be taught all the “why’s” about fractions, but this often doesn’t happen. I will cover some of that here.
Ways to think about fractions
First of all, any fraction, in and of itself, is an act of division. In any fraction, the numerator (the top) is divided by the denominator (the bottom). This is particularly easy to see in an improper fraction (a fraction in which the numerator is larger than the denominator); for example, the improper fraction 20/5 means twenty divide by five, so it equals 4.
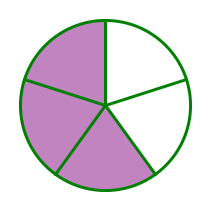
This is a little less intuitive for a more typical fraction, such as 3/5. What exactly does it mean to divide three by five? Well, think of it this way. Suppose you had three pies, and these three pies had to be divided equally among five hungry individuals. The way to do this would be to cut each of the three pies into five equal pieces, and then give each person three of those pieces. Thus, each person would get exactly 3/5 of a pie.
The pie metaphor is very important. The fraction 3/5 also means that we slice the pie in five pieces and then select three of these five.
It’s very important to think about this when you are reasoning with fractions, because whenever you can involve the visual portion of your brain, you understand math more deeply.
This also bring up another important thing to understand about any fraction. Mathematicians are, in some sense, a bit casual about writing one number over another. One thing that 3/5 means is that we have three of these things called a fifth. More properly, it would be written as the number 3 times the fraction 1/5, but as a kind of abbreviation, mathematicians just write this as 3/5. This means you always need to recognize, for any fraction, that the numerator is how many of the things you have, and these things are one over the denominator. Thus
If you can have all three of these perspectives at once—the division perspective, the slices of pie visual, and the numerator as a multiplier—then the logic of fractions will really start to make sense.
Notice that, right away, we could compare the size of two different fractions. If two fraction have the same denominator and different numerators, then the one with the larger numerator has the larger value: 5/7 > 4/7. We have more of the same things. By contrast, if two fraction have the same numerator and different denominators, the one with the larger denominator has a smaller value, because we are dividing by more. If we divide the same three pies equally among eight people, everyone gets slightly less pie than they would have gotten if the same pies had been divided equal among seven people: 3/8 < 3/7.
Adding and subtracting
It should be clear that if we take 3 of any thing, and add 5 of that same thing, we have 8 of that thing. This basic idea is known in mathematics as the Distributive Law. It doesn’t matter what the “thing” is. We could add 3 eggs to 5 eggs, or $3 to $5, or 3 people to 5 people, or 3 days to 5 days. In each case, the sum would be 8. Even though we could have an infinite number of different individual items, the formal mathematical process is the same.
Well, when we have 3/11 and 5/11, then we have three of a thing and five of the same thing, so it must be true that we can add them in exactly the same way we add everything else.
3/11 + 5/11 = 8/11
Similarly,
3/7 + 2/7 = 5/7
1/9 + 7/9 = 8/9
Also,
9/13 – 7/13 = 6/13
4/5 – 3/5 = 1/5
We can add or subtract fractions that have the same denominator in exactly the same way we add or subtract eggs or dollar or people or anything else. It’s exactly the same formal process, and once again, this formal process is known as the Distributive Law.
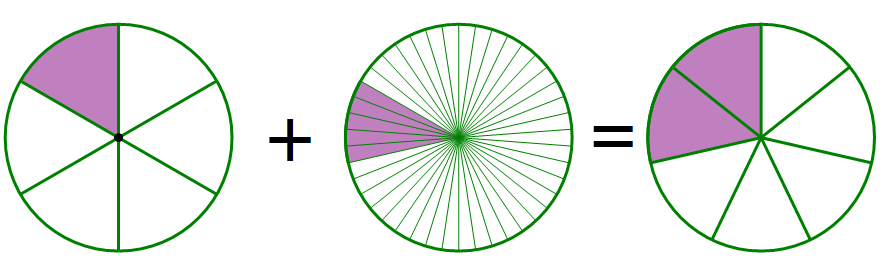
That’s great when the two fractions that we to have to add or subtract happen to have the same denominator. Often, though, we are not quite so lucky.
Here, we need to go back to the idea of fractions as division. Anything (other than zero) divided by itself equals one. This immediately implies that if we make a fraction in which the numerators equals the denominator, that fraction will have to equal 1. We could make any an infinite number of different fractions equal to 1, if we so chose. Of course, one of the many remarkable properties of one is that we can multiply anything by it, and the value of thing doesn’t change. Multiplication by one preserves the identity of any quantity.
Well, suppose we had to perform the following subtraction.
Notice that we know that the first fraction is larger, because it has a smaller denominator. Here, we were not lucky enough to get two fractions with the same denominator. Instead, we need to form common denominators, so we can do ordinary subtraction. Here, we can multiply the first fraction by 4/4 (a fraction that equals one), and multiply the second by 3/3. Since each is multiplied by 1, neither changes its value. Then we can subtract.
For simple cases, we can just use the two denominators to make our something-over-itself fractions. With slightly larger numbers, it pays to find the Least Common Denominator (LCD). The Magoosh math lessons discuss the process of finding the LCD for even large numbers. Those are the basics of adding and subtracting fractions.
Summary
Here, we covered some basic ideas about fractions as well as fraction addition and subtraction. If you had any insights while reading, you may want to give the practice question at the top another look before moving on to the explanations below. In the next post, we will cover fraction multiplication & division.
Practice problem explanation
1) Subtract (1/6) from both sides.
The common denominator is 42. To get this common denominator, we multiply the first fraction by (6/6) and the second by (7/7).
Answer = (D)

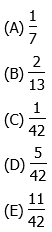




Leave a Reply