The AP Calculus AB Exam is one of two standardized tests in calculus that could translate to actual college credits. The AB exam covers roughly one and a half semesters of college-level calculus, while the BC exam covers about two full semesters (Calculus I and II). This article provides a brief guide on what to expect on the AP Calculus AB exam.
The AP Calculus AB Exam
The AP Calculus exams are typically offered once a year in May. You can expect to spend the entire morning at the testing center, as the exam take 3 hours and 15 minutes. There are two main sections, multiple choice and free response. In turn, each section consists of two parts, one that permits a graphing calculator and one that does not.
Format of the Exam
The Calculus AB and Calculus BC exams both have the same format.
| Section / Part | Type of questions | Number of questions | Time Limit | Calculator permitted? |
|---|---|---|---|---|
| IA | Multiple Choice | 30 | 60 minutes | No |
| IB | Multiple Choice | 15 | 45 minutes | Yes |
| IIA | Free Response | 2 | 30 minutes | Yes |
| IIB | Free Response | 4 | 60 minutes | No |
Topics on the AP Calculus AB Exam
The material on the exam falls into three main categories, limits, derivatives, and integrals. However these topics are all related. It’s not uncommon to encounter questions that require methods from all three areas.
Limits and Continuity
Limits measure trends in graphs. Typical topics within the area of limits and continuity include:
- Graphs of functions.
- Limits and continuity. Finding limits algebraically or estimating them from numerical or graphical data. Continuity in terms of limits.
- Intermediate Value Theorem and Extreme Value Theorem.
- Vertical, horizontal, and oblique asymptotes. Limits involving infinity.
Derivatives and Rates of Change
![]()
The derivative measures the slope of the graph at a point as well as rates of change. The following topics generally show up on the exam.
- Limit definition of the derivative and its relationship to continuity.
- Derivative rules.
- Slope and tangent lines.
- Linear approximation and differentials.
- Instantaneous and average rates of change. Relationship among position, velocity, and acceleration functions.
- Higher order derivatives.
- Implicit Differentiation.
- Analysis of Graphs based on both pre-calculus methods and derivative information.
- Mean value theorem and Rolle’s Theorem.
- Applications of derivatives, including optimization and related rates.
- Elementary differential equations and slope fields.
Integrals and Area
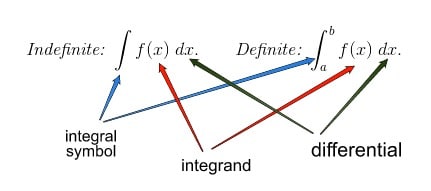
Integrals, antiderivatives, and their applications form the third major source of problems on the AP Calculus AB exam.
- Antidifferentiation and indefinite integrals.
- Techniques of antidifferentiation, including power rule, algebraic manipulation, and substitution.
- Finite Riemann sums and their limits. Relationship to definite integrals.
- The Fundamental Theorem of Calculus and definite integrals.
- Methods for estimating area.
- Exact area below a curve or between two curves. Average value.
- Volumes of solids of revolution.
- Accumulation functions.
- Relationships between position, velocity, and acceleration using integrals. Exponential models.
Scores and Credits
If you score a 4 or 5 on the AP calculus AB exam, then most colleges and universities will offer you 4-5 credits of calculus (single semester). Sometimes even a score of 3 will earn you credit for lower level courses such as Precalculus. However, schools differ in their AP policies, so always check out that information before applying.
More Information about the Exam
For more information, check out What is the AP Calculus AB Exam? and What Topics are on the AP Calculus AB Exam?.





Leave a Reply