You know you’ll have to know your derivatives inside and out in order to score high on the AP Calculus exam. But what are the most common derivatives you’ll see on the test? In this short article, we’ll let you in on the secret!
Know the Basics
First of all, it’s very important to have the basics down. That includes: the Power Rule, Product Rule, Quotient Rule, and Chain Rule, among others.
Don’t forget about those special functions either. You’ll have to memorize the derivative rules for trig, exponential, and logarithmic functions.
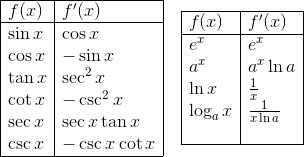
Less common, but no less important are the rules for inverse trig functions.

Check out Calculus Review: Derivative Rules and Derivatives on the AP Calculus AB & BC Exams: A Refresher for more.
Common Derivatives
Now let’s take a look at a few problems involving common derivatives that are modeled after actual AP Calculus problems.
Problem 1
Find The tangent line to the curve f(x) = x4 + 3x – 10 at the point (1, -6).
Solution
To find a tangent line, first take the derivative. Here, we have to use the Power Rule and Sum/Difference Rule.
f '(x) = 4x3 + 3
Then you can find the slope and the equation of the tangent line.
Slope at x = 1: f '(1) = 4(1)3 + 3 = 7
y – (-6) = 7(x – 1)
y = 7x – 13.
Problem 2
The position of a particle moving along the x-axis at time t is x(t) = sin( cos( 4t ) ), for 0 ≤ t ≤ π. Find
the velocity at time t = π/8.
Solution
Find velocity by taking the derivative of the position function. Be careful — we need two applications of the Chain Rule for this one!
v(t) = x '(t) = cos( cos( 4t ) ) ( -sin( 4t ) ) (4)
At time t = π/8, the velocity is equal to:
v(π/8) = cos( cos( 4(π/8) ) ) ( -sin( 4(π/8) ) ) (4) = cos( cos( π/2 ) ) ( -sin( π/2 ) ) (4)
= cos(0)(-1)(4) = (1)(-1)(4) = -4.
Problem 3
Find all inflection points of the curve defined by ![]() .
.
Solution
You can find inflection points by taking the second derivative. Of course, you must take the first derivative first. Don’t forget to rewrite your radical as a power and use Chain Rule.
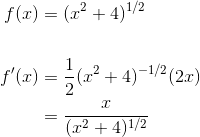
Use Quotient Rule to help find the second derivative.
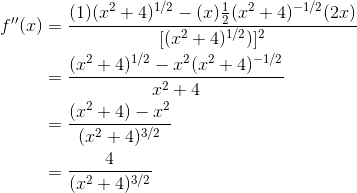
After simplification, we find that the second derivative is never equal to 0 and never undefined. Therefore this function has no inflection points.
Problem 4
![]()
Solution
You’ll need both the Product and Chain Rules for this one.
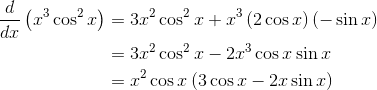
Problem 5
Suppose g(x) = e4x + 5. At what value of x is the slope of the tangent line to g(x) equal to 3?
Solution
Again, the slope of the tangent line is equal to a derivative value.
g '(x) = 4e4x
Set g '(x) = 3 and solve:
4e4x = 3
e4x = 3/4
4x = ln(3/4)
x = ln(3/4) / 4 ≈ -0.0719
Summary
The five problems above represent just a small sampling of what you’ll find on an AP Calculus AB or BC exam. Nevertheless, the majority of problems involving derivatives do tend to fall into these basic formats.
- Know your basic rules, especially the Chain Rule.
- Memorize the derivatives of the special functions.
- And above all, know which tools apply in each situation.
Good luck on the exam!





Leave a Reply