Problems concerning horizontal asymptotes appear on both the AP Calculus AB and BC exam, and it’s important to know how to find horizontal asymptotes both graphically (from the graph itself) and analytically (from the equation for a function).
Before we delve into finding the asymptotes though we better see what exactly an asymptote is.
Definition of Horizontal Asymptote
A horizontal asymptote for a function is a horizontal line that the graph of the function approaches as x approaches ∞ (infinity) or -∞ (minus infinity). In other words, if y = k is a horizontal asymptote for the function y = f(x), then the values (y-coordinates) of f(x) get closer and closer to k as you trace the curve to the right (x→ ∞) or to the left (x → -∞).
The Limit Definition for Horizontal Asymptotes
Because asymptotes are defined in this way, it should come as no surprise that limits make an appearance. The precise definition of a horizontal asymptote goes as follows: We say that y = k is a horizontal asymptote for the function y = f(x) if either of the two limit statements are true: ![]() .
.
Finding Horizontal Asymptotes Graphically
A function can have two, one, or no asymptotes. For example, the graph shown below has two horizontal asymptotes, y = 2 (as x→ -∞), and y = -3 (as x→ ∞).
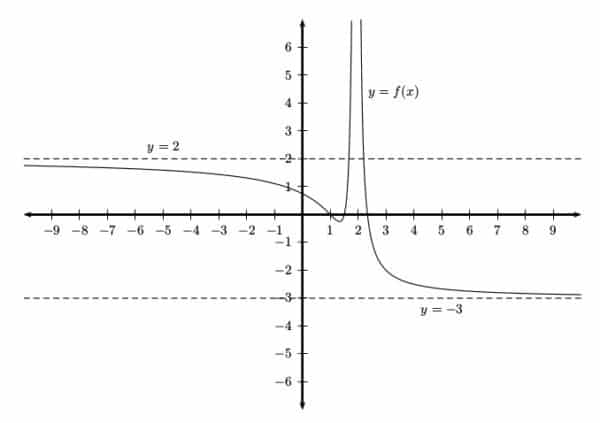
If a graph is given, then simply look at the left side and the right side. If it appears that the curve levels off, then just locate the y-coordinate to which the curve seems to be approaching. It helps to sketch a horizontal line at the height where you think the asymptote should be. Let’s see how this works in the next example. Keep in mind, you will typically not be shown the dashed line — that would make the problem way too easy!
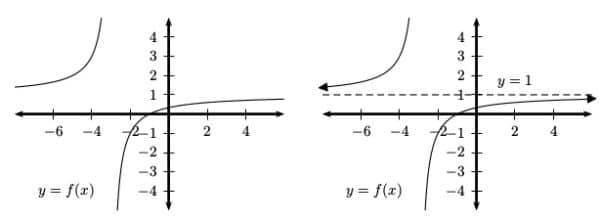
The graph on the left shows a typical function. If you follow the left part of the curve as far to the left as you can, where do you end up? In other words, what is the y-coordinate of the leftmost point shown in the graph? A good estimate might be somewhere between 1 and 2, perhaps a little closer to 1.
Well imagine what would happen if you continued drawing the graph to the left of what is shown. It seems reasonable that the curve levels off and approaches a value of 1, gently touching down on the horizontal line y = 1 just like an airplane landing.
Similarly, follow the right part of the curve as far to the right as you can, and imagine what would happen if you kept going. Again, the curve seems to level off and approach y = 1, this time coming up from below the line. This function has a single horizontal asymptote, y = 1. Once you sketch the line (dashed in the righthand figure), it becomes clear that we have found the correct horizontal asymptote.
Finding Horizontal Asymptotes Analytically
What if you are not given a graph? Well in many cases it’s actually quite easy to determine the horizontal asymptote(s), if any exist. There are just a few rules to follow.
Rational Functions
If your function is rational, that is, if f(x) has the form of a fraction, f(x) = p(x) / q(x), in which both p(x) and q(x) are polynomials, then you can use highest order term analysis. The highest order term of a polynomial p(x) is the single term having the greatest degree (exponent on x). For example, the highest order term of 6x – 3x5 + 5x3 + 42 is: –3x5.
Highest Order Term Analysis
To do highest order term analysis on a rational function, make sure the top and bottom polynomials are fully expanded and then write a new function having only the highest order term from the top and from the bottom. All other terms (lower order terms) can safely be ignored. Cancel any common factors and variables and:
-
If the result is a constant k, then y = k is the single horizontal asymptote. This happens when the degree of the top matches the degree of the bottom.
-
If the result has any powers of x left over on top, then there is no horizontal asymptote.
-
If the result has any powers of x left over on bottom, then y = 0 is the single horizontal asymptote.
Examples for Highest Order Term Analysis
Let’s use highest order term analysis to find the horizontal asymptotes of the following functions.
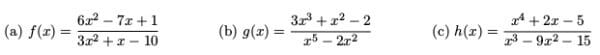
(a) The highest order term on the top is 6x2, and on the bottom, 3x2. Dividing and cancelling, we get (6x2)/(3x2) = 2, a constant. Therefore the horizontal asymptote is y = 2.
(b) Highest order term analysis leads to (3x3)/(x5) = 3/x2, and since there are powers of x left over on the bottom, the horizontal asymptote is automatically y = 0.
(c) This time, there are no horizontal asymptotes because (x4)/(x3) = x/1, leaving an x on the top of the fraction.
Exponential Functions
The method of highest order term analysis is quick and easy but only applies to rational functions. What if you are given a different kind of function? Certain functions, such as exponential functions, always have a horizontal asymptote. A function of the form f(x) = a (bx) + c always has a horizontal asymptote at y = c. For example, the horizontal asymptote of y = 30e–6x – 4 is: y = -4, and the horizontal asymptote of y = 5 (2x) is y = 0.
Horizontal Asymptotes in General?
More general functions may be harder to crack. However, just remember that a horizontal asymptote are technically limits (as x→ ∞ or x→ -∞). Therefore, they measure the end behavior of the function. If you are working on a section of the exam that allows a graphing calculator, then you may simply graph the function and trace it to the right and left until you can determine whether the values level off in either direction.
Conclusion
Problems about horizontal asymptotes are usually not too difficult. Know how to look at the graph, or if a graph is not given, then know how to analyze the function (highest order term analysis for rational functions, the special rule for exponential functions, or when all else fails, try graphing).

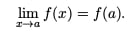


Leave a Reply