AP Calculus Review: Indefinite Integrals

Indefinite integrals make up a substantial part of what is covered on the AP Calculus AB and BC exams. In this review article, we highlight a few concepts and techniques that you’ll need to be familiar with.

What are Indefinite Integrals?

There are two kinds of integrals, the definite and indefinite integrals. This article only discusses indefinite integrals. For a more general overview, including information about definite integrals, check out this review of integrals.

An indefinite integral of a function f is the most general antiderivative of f.

Here, the function F is any particular antiderivative for f. That is, F ^‘(x) = f(x). For example, F(x) = x² is an antiderivative for f(x) = 2x, since (x²)’ = 2x.

The C is the constant of integration. It stands for any constant, and it must be part of your answer to an indefinite integral.

So for example,

What’s the Deal with the “ + C ” Anyway?

The reason we need to tack on that “ + C ” is so that we can describe absolutely every antiderivative for f. Remember the derivative rule for constant functions:

Therefore, if there is a particular function F(x) such that F ‘(x) = f(x), then for any constant C, we have:

Thus the most general antiderivative of f(x) would be F(x) + C.

Indefinite Integral Techniques

Most everyone knows that you shouldn’t use a screwdriver to pound in a nail. And hammers do not help when driving in screws. In a similar way, you should be aware that each indefinite integral problem requires its own set of tools.

We’ll discuss a few integration tools, including the basic antiderivative rules, substitution, integration by parts, and partial fractions. Other more advanced tools may be covered in future Magoosh articles.

Also, it’s important to realize that each technique requires quite a bit of practice before you can really get good at it. Don’t expect to become an expert on the first day.

Basic Antiderivative Rules

These rules are really just derivative rules in reverse. Here is a list of the basic antiderivative rules.

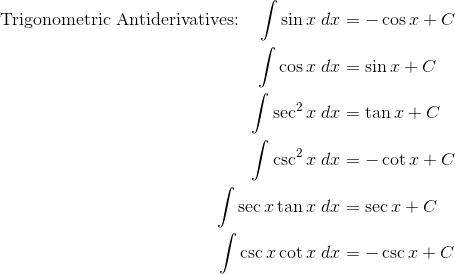
Substitution

The Substitution Rule, or as it’s more commonly known, u-substitution, is a rule that “reverses” the Chain Rule.

This rule helps when the integrand is a composition of two functions. That is, if there is a function inside another function. For example, we would identify (5x + 1)⁸ as a composition of the functions u = 5x + 1 and f(u) = u⁸. So if we needed to know the indefinite integral of (5x + 1)⁸, we could use substitution.

Steps for Substitution

Substitution can be difficult because the formula requires a specific setup. However, if you follow the steps outlined below, then you’ll be sure to get it right every time.

1. Identify a part of the function that you will try to substitute, and write it down: u = g(x). It may not be obvious what to pick, so don’t be afraid of a little trial and error at first.
2. Take the differential of your substitution. That is, find the derivative of g and write it in the form, du = g ‘(x) dx.
3. Substitute both u and du into the original integral. This may involve solving the differential for dx and then replacing the dx in the integral.
4. If the new integral involves only u and du, then simplify and integrate using standard methods.
5. Finally, plug u = g(x) back in so that your answer is in terms of the original variable x.

Using the Substitution Rule

First we must decide what to substitute. Experience tells us to look for expressions within parentheses.

Don’t forget to take the differential. I find it helpful to solve for dx.

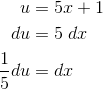
Now you can replace 5x + 1 by u and dx by (1/5)du. Then integrate and finally plug back in u = 5x + 1.

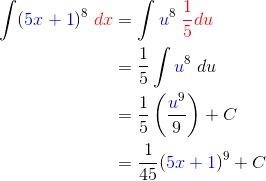
Integration by Parts

Integration by Parts (IBP) is a powerful method that may be used when there are certain kinds of products in the integrand. In fact, you can think of IBP as a way to “reverse” the Product Rule.

Suppose u and v are differentiable functions of x. Then the IBP formula states that:

Example Using IBP

Typically we use IBP when there are products of powers of x, exponential functions, and/or trigonometric functions in the integrand.

Here we will choose u = 3x, and dv = cos x dx. Again, experience guides our choices. If you had chosen the functions the other way around, then the integral would have gotten more complicated.

Now find du by taking a derivative, and v by integrating.

Next, we use the IBP formula to rewrite the original integral in a different way. Try to track where u, v, du, and dv show up in the problem. (Hint: They’re color coded.)

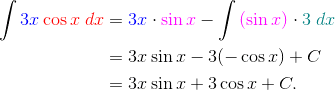
Partial Fractions

Last but not least, let’s talk about the method of Partial Fractions (PF). We can use PF whenever the integrand is a rational function whose denominator has a degree of at least 2. The main idea is to break apart the fraction into a sum of simpler fractions.

In this short review, there is not enough time to explain all of the details. So if you’re interested in learning more, check out this article.

Instead, let’s see a quick example of the technique in action.

The key is to use your algebra skills to factor the denominator and split into two fractions, solving for the unknown constants in each numerator.

It can be determined that A = -2 and B = 3 in this example. Again, because this article is just review, we leave some of the details to you.

Now we can work out the problem completely.

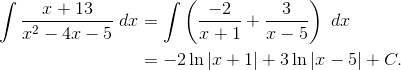
Summary

Indefinite integral problems come in many different types on the AP Calculus Exams. Remember that an indefinite integral is the most general antiderivative of a function.

Among the wide range of techniques available, most problems can be handled by one or more of the following methods.

• Basic antiderivative formulas, including the Power Rule and rules for special kinds of functions (such as trigonometric and exponential).
• Substitution
• Integration by parts
• Partial fractions

After much practice, you will be able to choose the best technique for each integral problem. Just like a good carpenter, using the right tool makes the job easy. You may even come to enjoy the challenge of indefinite integrals!