The derivative is the basis for much of what we learn in an AP Calculus. This article will go over all the common steps for determining derivatives as well as a list of common derivative rules that are important to know for the AP Calculus exam.
Understanding the definition of derivatives
Before we memorize the derivative rules, when studying for the AP Calculus exam, first make sure that you understand the definition of a derivative from the very beginning. Questions will certainly arise on the exam which ask you a bit about what to expect will happen to the slope between two points, as those points get closer together on a curve. The definition of a derivative:
![]()
You should be able to clearly explain what is happening in this equation, why it is important, and how to use it.
There is a jump here between our definition, and how we often determine derivatives. By the time you get to the AP exam, you need to be very comfortable finding derivatives with the power rule, product rule, quotient rule, and chain rule. As well, you should know a few of the most common derivatives (the 6 trig functions, exponential functions, and logarithm functions). You do not need know how these formulas are created from the definition of the derivative given above, but it is certainly a good exercise to do in your calculus class.
On the AP exam, the derivative is used for many different types of problems.
Some of the most common derivative questions will involve:
- Determining the equation of a line tangent to a curve at a point.
- Determining if a function is increasing or decreasing at a given point.
- Determine the critical points of a graph.
- Determining rate of change of physical systems. This involves understanding how velocity
and acceleration of a particle is related to the position of that particle changing with time. - Determining the minimum and maximum of a function.
- Using L’Hopital’s rule to determine limits of functions (ex: find the lim as x goes to 0 of sin(x)/x)
Derivative Rules
Constant Rule:
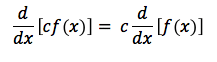
Rule of Sums:
![]()
Rule of Differences:
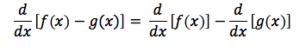
Product Rule:
![]()
Quotient rule:
![]()
This can also be thought of as the product rule with 1/g(x)
Power Rule:
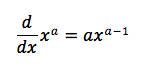
Chain Rule:
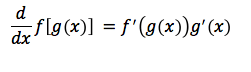
Examples of Derivative Rules Use:
![]()
This is two functions multiplied by each other, so we use the product rule:
![]()
![]()
This is a function of a function, so we use the chain rule:
![]()
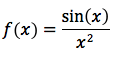
This is a division of two functions, so we we look toward the quotient rule:
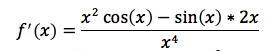
Notice, this is the same thing as saying ![]() , which we can solve with the product rule.
, which we can solve with the product rule.
![]()
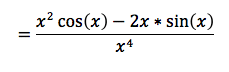
Common Derivatives
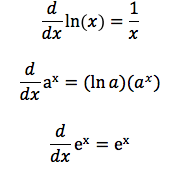
Common Trig Derivatives
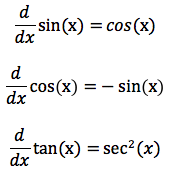
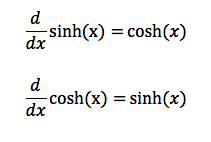
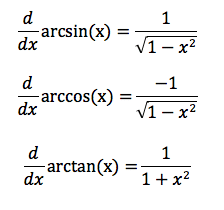





Leave a Reply