Antidifferentiation is an essential tool for evaluating integrals. In fact, you might say that antidifferentiation is pretty much the same thing as finding an indefinite integral.
When we antidifferentiate a function, we are simply finding another function whose derivative is equal to the one we started with.
What is Antidifferentiation?
Antidifferentiation is the reverse of differentiation. So just as differentiation is the process of finding a derivative, antidifferentiation is the catch-all term for any formula, technique, or method of finding an antiderivative.
If f is a function, then we say that F is an antiderivative for f if F '(x) = f(x).
How Many Antiderivatives Can a Function Have?
If a function has one antiderivative, then it has infinitely many antiderivatives. This is because the derivative of any constant is 0. So if F(x) is an antiderivative of f(x) and C is any constant, then
[F(x) + C]' = F '(x) + [C]' = f(x) + 0 = f(x).
Therefore, F(x) + C is also an antiderivative for f. We call C the constant of integration.
Notation and Relationship to Integral
The indefinite integral of a function f is, by definition, the most general antiderivative of f. Notation for the indefinite integral is shown below.
![]()
Whenever we work out an indefinite integral, we are doing antidifferentiation.
Antidifferentiation Formulas
There are many more formulas and techniques for antidifferentiation. Fortunately you only need to be aware of the basics for both the AB and BC exams.
The AP Calculus AB exam covers basic antidifferentiation formulas and substitution of variables.
The AP Calculus BC exam includes not only the basic formulas and substitution but also integration by parts (IBP), and simple partial fractions (PF). This test also has more challenging problems overall.
Note, these rules are all written in terms of indefinite integrals.
The Basic Rules
The “basic” rules refer to those rules that follow directly from differentiation rules. Some of the more common rules include the Power Rule, Sum/Difference Rule, and Constant Multiple Rule. There are also rules for certain trigonometric, exponential, and other elementary functions.
![]()
![]()
![]()
![]()
![]()

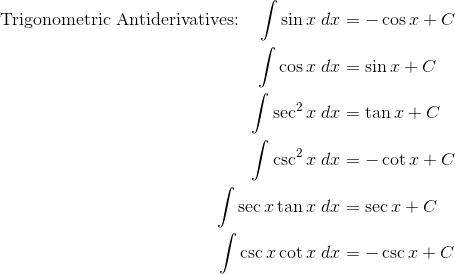
Substitution Rule
The Substitution Rule, or u-substitution, is a rule that “reverses” the Chain Rule.
![]()
Integration by Parts
Integration by Parts (IBP) is a powerful method that may be used when there are certain kinds of products in the integrand. In fact, you can think of IBP as a way to “reverse” the Product Rule.
Suppose u and v are differentiable functions of x. Then the IBP formula states that:
![]()
Partial Fractions
The method of Partial Fractions (PF) is an specialized technique for rational functions. The main idea is to break apart the fraction into a sum of simpler fractions.
Fortunately, even on the BC exam, you only need to know the easiest cases of PF. In the simplest cases, the denominator factors into unique linear factors.
- Step 1. Factor the denominator. Each of those factors will become the denominator of its own fraction.

- Step 2. Then you will have to determine the constant numerators. There are various algebraic ways to do this. Perhaps the quickest and easiest way is the Heaviside cover-up method.
When there are only linear factors, the Heaviside cover-up method works as follows:
For each factor (x – c) cover that factor in the expression. Then plug the root of that factor (that is, x = c) into the remaining expression. The result is the correct value of the constant A corresponding to that factor.
- Step 3. Finally, integrate each simpler fraction. In the easiest cases, this involves a simple substitution and the rule for 1/x. Each fractional term follows the same basic rule:

Practice Problems
Let’s do some antidifferentiation!
Example 1
Find the antiderivative of 4x3 – 8x + 7.
This is a job for the basic rules, including power rule.
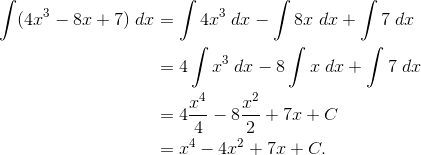
Now let’s check our work. Remember, antidifferentiation is the reverse of differentiation. So all you have to do is find the derivative of your answer and verify that it is the same as the original integrand.
![]()
Example 2
![]()
This is a job for partial fractions. First, verify the numerator has smaller degree than the denominator. (If it had the same or larger degree, then you would first have to rewrite the integral using polynomial division. Check out this video to learn more about long division of polynomials.)
First factor the denominator. x2 – 7x + 12 = (x – 3)(x – 4).
Next, rewrite the integrand as a sum of fractions with each factor as denominator and unknown constant as numerator.
![]()
Now use the Heaviside cover-up method for each factor.
![]()
![]()
Finally, plug your constants in and integrate.
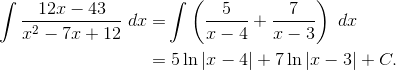
Summary
Antidifferentiation is the reverse of differentiation. It is the same as finding an antiderivative for a function. The indefinite integral is the most general antiderivative. The antidifferentiation techniques required on the exams include:
- Basic formulas
- Substitution
- Integration by Parts (BC only)
- Partial Fractions (BC only)





Leave a Reply