AP Calculus Review: Differential Equations

A differential equation is a relation that involves an unknown function and its derivative. There are many kinds of differential equations and tons of specialized techniques we may use to solve them. Fortunately, on the AP Calculus exams you will only encounter a handful of the most basic kinds.

Basic Differential Equations: Integration

You have probably worked out hundreds of differential equations without even realizing it!

It’s true! Let me give you an example.

What makes this a differential equation?

Well think about what the notation means. You know that integration is the opposite of differentiation. So what we’re looking for here is a function f(x) whose derivative is equal to 2x. In other words, we have to solve:

f ‘(x) = 2x

That’s a relation involving an unknown function f and its derivative.

But this differential equation is trivial to solve! Just use the power rule for integrals (or guess-and-check).

f(x) = x² + C

(For a full review of integration, check out: AP Calculus Exam Review: Antidifferentiation or AP Calculus Exam Review: Integrals.)

Initial Value Problems

Now suppose you have more information about an unknown function, such as its value at a certain point. Then you may be able to solve for the function explicitly, rather than getting stuck with an unknown constant of integration at the end.

An initial value problem typically gives a derivative expression along with a function value. The goal is to produce the original function.

Example 1: Initial Value Problem

If f ‘(x) = 1/x² for x > 0, and f(1) = 5, find the expression for f(x) for x > 0.

Solution

Because the derivative expression is given, we integrate to find the original function. Don’t forget about your constant of integration!

Next, plug in the known info and solve for the unknown constant of integration.

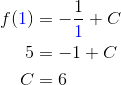
This implies that the original function must be:    f(x) = -1/x + 6.

Separation of Variables

Of course not every differential equation (or DE) problem can be handled by simple integration. Often more advanced techniques must be used, especially if both x and y show up in the equation.

For example, the following DE cannot be cracked by integration (…not in its current form, that is).

The key is to somehow break up the dy and dx.

The derivative notation dy/dx looks like a fraction. However, it’s not really a fraction, because the two quantities dy and dx (called differentials) are supposed to represent the idea of taking Δx to zero in the limit. In other words, if you had to identify the numerical “value” of a differential, it would make sense to say dx = dy = 0. And we all know that 0/0 is undefined.

But those differential gadgets are more subtle than that. They really don’t carry a numerical value. Instead, they stand for a limiting process. And if we’re very careful, we can work with dx and dy individually.

The method of Separation of Variables works by manipulating dy/dx as if it were a fraction, and then using integration to get rid of the differentials.

Now let’s take another look at our example above.

Example 2: Separation of Variables

If    , and y(0) = -3, find an equation for y in terms of x.

Solution

First multiply dx to both sides. Then multiply or divide as necessary so that only expressions of y are on the left, and only those with x are on the right.

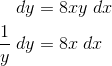
Next, we use the magic of calculus! All you have to do is to apply the integral symbol to each side of the equation. Now you have two separate integrals to work out.

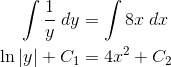
Now even though both sides generated a constant of integration, those can be combined into a single constant on the right hand side. The next few steps are just for isolating y.

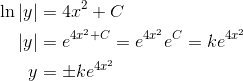
Notice that the quantity e^C is replaced by another constant k. This is because C is still arbitrary (and unknown). So just think of k as a related, but still arbitrary constant.

Finally we solve for k using the known information, y(0) = -3.

(By the way, we will drop the “±” notation at this point because k itself can take care of that choice.)

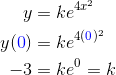
Therefore, replacing k by its computed value -3, we obtain the final form of the function.

Setting Up Differential Equations

Fortunately you won’t encounter any DE problems on the AP Calculus exam that can’t be handled by either integration or separation of variables.

However, you may be asked to set up and/or analyze a DE (without solving it).

Example 3: Setting up a DE

A certain bacteria culture has P cells at time t and grows in proportion to the square root of the amount present. Set up a differential equation that models A(t).

Solution

Because the culture grows at a certain rate with respect to time, we know we’ll be working with the derivative dA/dt.

Let k be the constant of proportionality. Then translate the given information into mathematics:

dA/dt = k × √(A)

Remember, we don’t have to solve for A(t); just set up the DE that could be used to solve for it. So we’re done at this step!

Example 4: Analyzing a DE

The number y of people infected with the flu in a certain town at time t can be modeled by the differential equation, dy/dt = 0.00002y(21500-y), where y(0) = 1. Determine the limit of y as t → ∞.

Solution

It would be difficult to solve this DE for y explicitly. Instead, look closely at the equation. It has the form of a logistics equation.

That means we can answer this question with no work at all! You just have to remember that logistics equations always have solutions that tend toward the carrying capacity M as t → ∞. Here, M = 21500. That’s all you need to answer the question!

The limit will be 21500.

(For more details about the logistics equation, I recommend: AP Calculus BC Review: Logistics Growth Model.)

Conclusion

Differential equations show up only sparingly on an AP Calculus exam. But it’s important to be aware of the techniques for solving them, setting them up, and analyzing them.

• Remember the basic methods of integration and separation of variables.
• Know how to set up a differential equation.
• Look for situations in which you may avoid solving the DE.