So the AP Calculus AB exam is coming up. Are you prepared? With this Calculus AB cram sheet, you can check that you have the skills necessary to score a 5 on the test.

About the Test
The AP Calculus AB exam is a 3 hour and 15 minute standardized test. A high score (4-5) typically qualifies you to receive college credit or equivalency for one full semester of calculus. So it’s really important to do well on the test if you want a jump start on your college career.
Click here to learn more about the format of the exam: What is the Format of the AP Calculus AB Test?.
General Tips
- Each section has two parts: calculator and no calculator. Make sure you have a good graphing calculator and are familiar with its features.
- Multiple Choice: There are a total of 45 multiple choice questions in one hour and 45 minutes. That gives an average of 2 minutes and 20 seconds per problem.
- Be sure to fill in your answers to the multiple choice problems completely on the bubble sheet.
- It doesn’t hurt your score to guess if you have no idea how to do a problem. But try to eliminate wrong answers first.
- Pace yourself. Do not spend too much time on any given multiple choice problem. If you find yourself spending too much time on a question, skip it and move on.
- On your first pass through the problems, answer what you can. Then take a second pass, if time permits.
- On your second pass, make sure that your bubble sheet accurately records what you think the answers are. Also, spend some time on more challenging questions that you couldn’t crack the first time around.
- Free Response: There are 6 free response problems in 90 minutes. So you have 15 minutes per question on average.
- Each free response question has 3 or 4 parts.
- In the free response section, spend enough time to clearly write out each step. Most of your points will be earned by showing and carrying out proper methods for each problem. Explain, communicate, and justify.
- After answering each question, re-read the question statement to ensure that you’ve understood what they were asking.

What Topics are Covered?
A detailed list of what’s on the test can be found here: What Topics are on the AP Calculus AB Exam?. In what follows, we will highlight a few of the definitions, properties, theorems, and formulas that may be useful on the test.
Basically, the AP Calculus AB exam covers three Big Ideas from calculus.
- Limits and Continuity
- Derivatives and Their Applications
- Integrals and Their Applications
AP Calculus AB Cram Sheet
Nothing can take the place of consistent study and review over a period of many weeks or months. Cramming the night before will not help you to raise your score.

So think of the following AP Calculus AB Cram sheet as a way to summarize and review what you (should) have been studying throughout the year.
Pre-Calculus Concepts
Mathematics tends to build upon earlier mathematics, and calculus is no different.
- General problem solving strategies. This includes using context clues and identifying the givens and the goals of a problem.
- Logic. Strong helps to piece together various approaches to a given problem and helps in using theorems and properties.
- Arithmetic. A large part of the exam does not allow a calculator. You’ll have to know how to add, subtract, multiply and divide numbers, including fractions and decimals. So if you’ve relied on your calculator all throughout high school, now is the time to get back to basics.
- Algebra. This includes simplifying and interpreting algebraic expressions as well as setting up and solving algebraic equations. (Yes, there’s a difference — An equation has an equals sign, while an expression does not.) Be familiar with the properties of exponents, logarithms, radicals, etc.

- Geometry. Know your basic perimeter, area, volume, and related formulas. Follow this link for a comprehensive formula sheet.
- Trigonometry. Definitions must be memorized (“SOH CAH TOA“) as well as the most often used trig identities. See AP Calculus Review: Trigonometric Identities for more details.
- Pre-Calculus. Know how to graph functions and how to interpret graphs. Be very familiar with linear functions, especially the concept of slope.
Big Idea 1. Limits and Continuity
- Know how to find limits algebraically or by estimating from numerical or graphical data.
- Definition of continuity in terms of limits. Check out Limits and continuity.
- Intermediate Value Theorem (IVT)
If f is continuous on a closed interval [a, b], and if L is any number between f(a) and f(b), then there is at least one value x = c on the interval such that f(c) = L.
- Extreme Value Theorem (EVT)
If f is continuous on a closed interval [a, b], then f attains both an absolute maximum and minimum value on the interval.
- Limits whose values are infinite and their relationship to vertical asymptotes
- Limits as x → ±∞ and their relationship to horizontal asymptotes
- Oblique asymptotes
Big Idea 2. Derivatives and Their Applications
- Limit definition of the derivative

- If a function is differentiable at a point, then it must also be continuous at that point. But not necessarily the reverse — for example, |x| is continuous at x = 0, but not differentiable there.
- Basic derivative rules.


- Derivatives of trigonometric, exponential, and logarithmic functions.

- Product Rule and Quotient Rule


- Chain Rule

- The tangent line to the curve y = f(x) at a point x = a is measured by the derivative: f '(a).
- If s(t) is a position function, then
- Velocity is v(t) = s '(t), and
- Acceleration is a(t) = s ''(t).
- Further topics and applications:
- Implicit Differentiation, Analysis of Graphs, including intervals of increase/decrease, relative minima/maxima, intervals of concavity, and inflection points.
- Mean Value Theorem and Rolle’s Theorem
- Optimization
- Related rates
- Elementary differential equations and slope fields
Big Idea 3. Integrals and Their Applications
- Rules and formulas of Antidifferentiation







- Integration by Substitution

- The Fundamental Theorem of Calculus (both parts)


- Area below a curve

- Area between curves, with f on top and g on bottom

- Volumes of solids of revolution by washer method and shell method.


- Further topics and applications:
- Estimating area or displacement by finite Riemann sums or Trapezoid Rule
- Average value of a function over an interval
- Models for exponential growth and decay
Note that you do not have to do integration by parts (IBP) or partial fractions on the AB test.
Final Thoughts
You can use this Calculus AB cram sheet as a checklist in order to ensure that you’ve done all of the necessary prep work. If you are reading this with plenty of time to spare before the exam, then consider setting up a 3-Month AP Calculus Exam Study Guide.
Best of luck on test day!


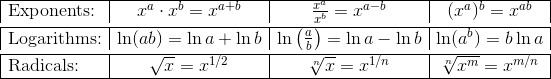
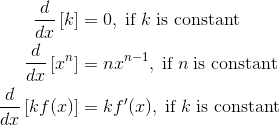
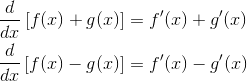
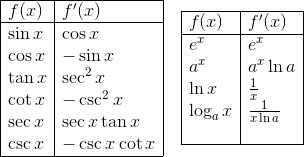

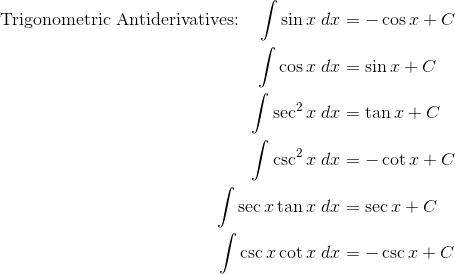




Leave a Reply