Mastering the Chain Rule

For the AP Calculus exam, whether it’s Calculus AB or Calculus BC, being completely fluent in taking the derivative of almost any function is imperative.  We should know how to use all the most common methods for taking the derive well enough that we don’t have to think about it on the exam itself.  The last thing we want to get caught up in on the exam is forgetting one of our derivative taking methods, such as the chain rule.

At minimum, you should know how to use:

• The power rule
• The chain rule
• The product rule
• The quotient rule

The chain rule is one of the most important rules in this list because many function cans be thought of as functions of functions (of functions of functions).

What is the chain rule and when do we use it?

 

The chain rule is used when we have a function which is of the form f(x) = g(h(x)).

For example:

Our function f(x) is made up of two smaller functions.  You can think of f(x) = g(h(x)), where h(x) = x² and g(x) = sin(x).  we can find the derivative of each of these functions individually.  The chain rule allows us to take the derivative of the entire thing.

The chain rule

 

In our above example, f(x) = sin(x²).   h(x) = x² , h’(x) = 2x, g(x) = sin(x), and g’(x) = cos(x).  The derivative of h(x) can be solved with the power rule, and the derivative of g(x) is a common derivative.  You can find a list of common derivatives as well as explanations of the other derivative rules in our review of derivative rules.

The difficulty in using the chain rule:

Implementing the chain rule is usually not difficult.  The problem that many students have trouble with is trying to figure out which parts of the function are within other functions (i.e., in the above example, which part if g(x) and which part is h(x).
This is going to be a rule which is very important to practice with over and over again.

A handful of example problems

Here is a list of example problems of varying difficulties.  You do not need a calculator to answer any of these questions.  You’ll find the solutions below.

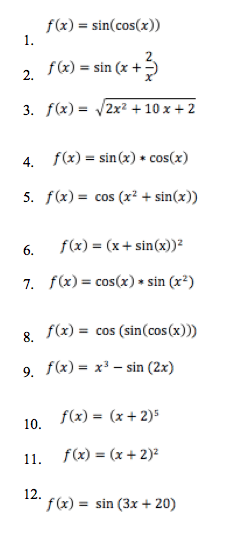
Solutions and Explanations to Example Problems

 

 1.

Solution:

 

2.

Solution:

 

3.

Solution:

 

4.

This one is thrown in purposely, even though it is not a chain rule problem.  Many students get confused between when to use the chain rule (when you have a function of a function), and when to use the product rule (when you have a function multiplied by a function).

Solution:

(This can be reduced to cos(2x) if you know your trig identities.)

 

5.

We can also use the chain rule in combination with the other rules.

Solution:

 

6.

Solution:

 

7.

Again, we can use chain rule in combination with other rules.

Solution:

 

8.

We can use the chain rule multiple times in a row as well.

Solution:

 

9. 

Solution:

 

10. 

Solution:

f'(x) = 5(x + 2)⁴

 

11. f(x) = (x + 2)²

Solution:

f'(x) = 2(x + 2)

 

12.

You will find that chain rule problems often involve sin, cos, and tangent, as we often use trigonometric along with other functions.

Solution:

 

Mastering the chain rule is incredibly important for success on the AP Calculus exam.  The key to studying the chain rule, as well as any of the differentiation rules, is to practice with it as much as possible.