The Quotient Rule is an important formula for finding finding the derivative of any function that looks like fraction. It is just one of many essential derivative rules that you’ll have to master in order to succeed on the AP Calculus exams. In this article I’ll show you the Quotient Rule, and then we’ll see it in action in a few examples.
The Quotient Rule
There are many different but equivalent ways to express the Quotient Rule.
Suppose f and g are differentiable functions. Then the quotient function, f/g is also differentiable, and
![]()
Or, in a more compact way (using letters u and v for the functions):
![]()
Finally, many textbooks give the following version using Leibniz notation. You may be familiar with the “Hi – Lo” trick that helps us to memorize it. “Hi” means the top (numerator) function, “Lo” is the bottom (denominator) function, and “De” tells you to take a derivative.
![]()
Relationship to Product Rule
The Quotient Rule and Product Rule share much in common. In fact, the two formulas are similar if you look at them the right way. (Unfortunately, most textbooks that I’ve seen do not write these formulas in the way that highlights their similarities.)
| Product | Quotient |
|---|---|
| f = uv | f = u/v |
| f ' = u'v + uv' | f ' = (u'v – uv')/v2 |
Notice that the quotient formula is just like the product formula except that there is a minus (-) in the middle instead of plus (+), and there is an added feature: denominator squared.
Example
Find the derivative of ![]() .
.
Identify the top and bottom functions,
u = x2 + 3x – 1.
v = x4 + 2.
It may help to write down the derivatives of u and v separately:
u' = 2x + 3.
v' = 4x3.
Then, using the Quotient Rule formula as a recipe, we have all the ingredients to cook up the derivative!
![]()
Now this is a correct but unsimplified derivative. Often on the AP Calculus test, your answers may not match the answer choices, simply because they have given their answers in simplest form. Let’s simplify our answer by multiplying through on the numerator and collecting like terms.
In order to help you see the steps, I’ve colored terms from the first product in blue, and those from the second in red.
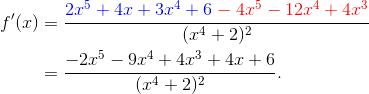
Example: Avoiding Quotient Rule
As much as we love the quotient rule, sometimes it’s just overkill. Sometimes a function has the form of a fraction but can easily be simplified to a non-fractional form. Then other derivative rules might be used instead of quotient rule.
Find the slope of the curve ![]() at x = 1.
at x = 1.
At first, this may look like a job for the Quotient Rule. However notice that the denominator has only a single term. The function can be simplified before taking the derivative.
![]()
Then take the derivative (because the derivative is the tool that measures slope).
![]()
Plug in x = 1 to find the slope: 8(1) – (1)-2 = 7.
Conclusion
If a function has the form of a fraction, then you may use the Quotient Rule to find its derivative, but also be on the lookout for easy simplifications that avoid having to use the rule.





