
Having trouble remembering your GRE math formulas on the fly? This free, downloadable GRE math formulas cheat sheet should help you! We’ll show you how to incorporate this GRE resource into your Quant prep below.
Although memorizing a GRE math formula (or twelve) isn’t the only way to study for GRE Quant, knowing certain frequently-tested formulas by heart will help you improve your speed on test day. Once you learn these formulas, be sure to practice using them! A little timed practice can go a long way.
Download our GRE math formulas cheat sheet PDF and read on to learn a little bit more about what to expect from the math section of the GRE.
Table of Contents
- How to Use the GRE Math Formulas Cheat Sheet
- Important GRE Math Formulas to Know
- GRE Math Formulas: Practice Problems
- Conclusion: Is This All You Need for GRE Math?
How to Use the GRE Math Formulas Cheat Sheet
Memorizing this GRE math formula cheat sheet is just the first step to mastering GRE math. Knowing which math formulas to use, then using them quickly and correctly, can really help you do well on GRE quant.
The GRE Quantitative Reasoning section tests concepts that you likely learned during sophomore and/or junior year of high school. These concepts DO NOT INCLUDE higher level math like trigonometry, calculus, or geometry proofs. They DO INCLUDE things you’ve probably long forgotten like properties of shapes, integer properties, exponent rules, and word problems.
The thing that takes these concepts to the GRE level is their complexity. Figuring out what each question is asking you to accomplish can be really tricky, whereas the math involved in solving them tends to be fairly straightforward. And you won’t get partial credit for showing your work, so picking the correct answer choice is very important! So study up the GRE math formulas cheat sheet and then practice using the formulas so you will know when they pertain to a question.
Important GRE Math Formulas to Know
Here are the most important GRE math formulas to know and practice before exam day!
Geometry
Squares
\(\text{Perimeter}=\text{4}\times\text{s}\), where s = side
\(\text{Area} = s^2\)
Rectangles
\(\text{Area} = \text{l}\text{w}\), where l = length and w = width
\(Perimeter = 2l+2w\)
Trapezoids
\(\text{Area}=\frac{Base1+Base2}{2}\times\text{height}\)
Polygons
\(\text{Total degrees}=180(\text{n}-2)\), where n = # of sides
Average degrees per side or degree measure of congruent polygon=\( 180(n-2)/n\)
Circles
\(\text{Area}=π\text{r}^2\)
\(\text{Circumference}={2}{π}\text{r}\)
\(\text{Arc Length}=\frac{x}{360}\times{2}{π}\text{r}\)
\(\text{Area of sector}=\frac{x}{360}\times{π}{r^2}\)
Triangles
\(\text{Area}=\frac{1}{2}\times\text{bh} \)
\(\text{Pythagorean Theorem}: a^2={b^2+c^2}\)
Divisibility
- 3 : sum of digits divisible by 3
- 4 : the last two digits of number are divisible by 4
- 5 : the last digit is either a 5 or zero
- 6 : even number and sum of digits is divisible by 3
- 8 : if the last three digits are divisible by 8
- 9: sum of digits is divisible by 9
Combinations and Permutations
\(nCr={n!}/{r!(n-r)!}\) n is the total number, r is the number you are choosing
\(nPr={n!}/{(n-r)!}\)
Read more about Combinations and Permutations.
Prime Numbers and Integers
- 1 is not a prime. 2 is the smallest prime and the only even prime.
- An integer is any counting number including negative numbers (e.g. -3, -1, 2, 7…but not 2.5)
Average
\(\text{Average}=\frac{\;\text{sum of n numbers}}{n}\)
\(\text{Average speed}=\frac{\;\text{total distance}}{\text{total time}} \)
Probability
\(\text{Probability of event}=\frac{\;\text{number of ways that fit the requirement}}{\text{number of total ways}}\)
Percentages
Percent Increase
\(\frac{\text{new amount-original amount}}{\text{original amount}}\times{100}\)
Percent Decrease
\(\frac{\text{original amount-new amount}}{\text{original amount}}\times{100}\)
Interest rate
Simple Interest
\(V= \text{P}({1+\frac{rt}{100})}\), where P is principal, r is rate, and t is time
Compound Interest
\(V= \text{P} (1+\frac{r}{100n}) ^{nt}\), where n is the number of times compounded per year
Distance, rate, time
\(D=rt\), \(Distance=Rate*Time\)
The Distance Formula
\(\sqrt{({x_2}-{x_1})^2+({y_2}-{y_1})^2}\)
Slope of a line
\(y=mx+b\)
GRE Math Formulas Practice Problems
1. Point A in the xy-coordinate system is shown below. Given two other points B (4a, b) and C (2a, 5b), what is the area of triangle ABC in terms of a and b?

Show answer and video explanation
Answer is E.
Click here to view the video explanation.
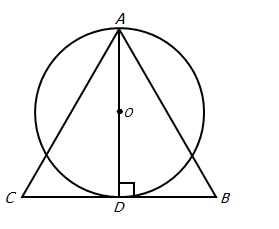
2. If the circle with center O has area 9π, what is the area of equilateral triangle ABC?
Show answer and video explanation
Answer is C.
Click here to view the video explanation.
3. The average (arithmetic mean) of 4 different integers is 75. If the largest integer is 90, what is the least possible value of the smallest integer?
Show answer and video explanation
Answer is E.
Click here to view the video explanation.
4. Ten students wrote a test, and the distribution of scores is shown on the frequency table. If the average (arithmetic mean) score is 62, what is the value of x?
| Score | Number of Students |
|---|---|
| 40 | 1 |
| 55 | 2 |
| 70 | 3 |
| x | 4 |
Show answer and video explanation
Answer is B.
Click here to view the video explanation.
5. In 2004, Cindy had $4000 in a mutual fund account. In 2005, the amount in the same account was $5000. If the percent increase from 2004 to 2005 was the same as the percent increase from 2005 to 2006, how much did Cindy have in this account in 2006?
Show answer and video explanation
Answer is C.
Click here to view the video explanation.
6. Tuk weighs 60 percent more than Kim, Lee weighs 50 percent less than Tuk, and Pat weighs 25 percent more than Lee. If Pat weighs 126 pounds, what is Kim’s weight?
Show answer and video explanation
Answer is 126.
Click here to view the video explanation.
7. In the xy-coordinate system, line k has y-intercept 12 and an x-intercept greater than zero. If the area of the triangular region enclosed by line k and the two axes is 30, what is the slope of line k?
Show answer and video explanation
Answer is A.
Click here to view the video explanation.
8. In the xy-coordinate system, line k has slope 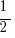 and passes through point (0, 5). Which of the following points cannot lie on line k?
and passes through point (0, 5). Which of the following points cannot lie on line k?
Show answer and video explanation
Answer is D.
Click here to view the video explanation.
Conclusion: Is This All You Need for GRE Math?
Like we mentioned before, simply memorizing these GRE math formulas is not enough. You’ll also need to practice so that you know when it’s appropriate to use each formula.
Magoosh GRE prep offers lesson videos and practice questions to help you learn to put these formulas to use. You can also choose between a live cohorted class with an instructor (which includes all our lessons and practice questions) or access to the self-study option by itself. And our Android/iPhone Prep App allows you to access that content on the go.
And even better than a cheat sheet—check out our free, downloadable GRE Math Formula eBook!




Leave a Reply