Most of the 56 questions on the Praxis Core Math test will be standard five-choice multiple choice, the same question format you have seen on standardized testing for most of your life. Those are not new to anyone. But, a handful of questions will be one of two other types:
- Multiple Answer questions
- Numeric Entry questions
Before I discuss these, here are a few examples of these alternate question formats.
1) The number line above shows the location of point A. Point B (not shown) is 2 units away from Point A, and Point C (not shown) is 3 units away from Point B. Which of the following could be coordinate of Point C?
Indicate all such answers.
[A] –6
[B] –2
[C] 0
[D] 2
[E] 4
[F] 6
x + 3 > 10 – 2x
2) Which of the following values of x are solutions of the inequality above?
Indicate all such values.
3) A triangle has sides 5, 13, and L. Which of the following could be the value of L?
Indicate all such values.
[A] 3
[B] 6
[C] 9
[D] 12
[E] 15
[F] 18
4) In the nation of Aplandia, the price before tax of a home entertainment is $400. Because this is a luxury item, Aplandia charges a 30% tax on this item. What is the total price with tax, in dollars?
5) What is the greatest common factor (GCF) of 54 and 81?
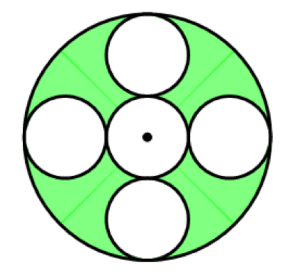
6) In the diagram above, all five smaller circles are exactly the same size, and the center of the middle circle is also the center of outer circle. The shaded region is what fraction of the area of the outer circle? Give your answer as a fraction.
Explanations will appear at the end of this blog article.
Two questions formats
As I said above, everyone knows how ordinary Multiple Choice works, because you have seen this on just about every standardized math test for your entire life. You will recognize the standard Multiple Choice if the directions say “Answer the question by clicking on the correct response.”
Notice that “correct response” is singular: only one answer is mathematically correct, and the other four are definitively wrong—this means you can use Process of Elimination on this kind of question. This question format will have ovals in front of the answers, and if you select one oval and then try to select another, the first gets de-selected. In other words, the computer makes it impossible for you to select more than one answer at a time in this format. In likelihood, between 45-50 of the 56 questions on the Praxis Core Mathematics test will be ordinary Multiple Choice questions.
A handful of the questions will be Multiple Answer questions. These have check-boxes next to the answer choices, instead of ovals, and the number of answer choices will vary: it could have five choices or more or fewer. These will contain the key phrase “Indicate all such values.”
The computer will allow you to check simultaneously as many or as few of these boxes as you like. On these, it may be that only one answer is correct, or it may be that all the answers are correct, or it may be that any possible subset of the answers are the correct ones. Your job is to make a decision for each and every choice: is each choice correct or incorrect? You can draw absolutely no inference from how many other answer choices are right or wrong: you have to consider each possible answer on its own. Not always, but many times you can establish some kind of range with a single calculation (as in #2 above), and then classify the answers according to this range, but sometimes you just have do a separate calculation for each possible answer.
Another handful will be the Numeric Entry questions. The dead-giveaway of this question format is there will be no answer choices at all in the window. You just get a question and an empty box, or if the answer is a fraction, you will have two empty boxes (as in #6 above). This is much more like ordinary high school math classroom math: you are given the problem, and you have to come up with the answer on your own.
You always can type your answer directly into the box. If you compute your answer using the onscreen calculator, then you can press the “Transfer Display” box at the bottom of the calculator and the computer will automatically transfer the display on the calculator to the answer box (this only works for single-box NE questions, not for the ones with two fraction boxes).
Summary
If you had any insights reading this article, you may want to give the question above a second look before reading the explanations below. You will only see a few of each one of these alternate question types on the Praxis Core Mathematics test, but it is important to be comfortable with the format so you are not caught off guard on test day!
Practice problem explanations
1) For this one, we need to figure out all the possibilities first, then find them among the answer. Point A is at x = –1. If Point B is two units away from Point A, it could be to the right or to the left: in other words, Point B could be at x = +1 or x = –3. We have to keep both of those Point B possibilities in mind when we consider the possible locations of Point C. Point C is 3 units away from either Point B, either to the right or to the left.
Point B at x = +1, 3 units to the right: Point C @ x = 4
Point B at x = +1, 3 units to the left: Point C @ x = –2
Point B at x = –3, 3 units to the right: Point C @ x = 0
Point B at x = –3, 3 units to the left: Point C @ x = –6
Those four are the possible locations of Point C. These correspond to the correct answers of (A), (B), (C), and (E).
2) For this one, we need to solve the inequality for x: doing so will establish a range for the possible correct values of x.
x + 3 > 10 – 2x
Add 2x to both sides.
3x + 3 > 10
Subtract 3 from both sides.
3x > 7
Divide by 3
![]()
Now, compare this to the answers.

Notice that, for (C) & (D), we could have compared the fraction parts larger than two: (1/2) is greater than (1/3), and (1/4) is less than (1/3). For (E), we didn’t need to compute anything about the square root of 10: we just had to realize that it is more than three. For (F), we know that pi is less than four, so if we divide by two, we see that pi divided by 2 has to be less than two.
Answers = (A), (B), (C), and (E)
3) For this one, we use the Triangle Inequality. The sum of any two sides of a triangle must be greater than the third side. Let’s say 13 is the longest side. Then
13 < 5 + L
8 < L
Notice that L could not equal 8, but it can have a value greater than 8. If L gets longer than 13, then L would be the longest side, and we need to consider this as well.
L < 5 + 13
L < 18
Again, L can’t equal 18. It has to be less than 18. The combined range for L is
8 < L < 18
The answers in this range are (C), (D), and (E).
4) Here, we can use some quick calculations so that we don’t have to use a calculator. We know that ten percent of anything is one tenth of it, so we can just lop off a zero.
10% of $400 = $40
Now, just multiply this by three.
30% of $400 = $120
That’s the tax. Add this to $400.
Total cost = $400 + $120 = $520
Answer = 520
5) If you have very good number sense, you might just be able to intuit the GCF, but as I discuss in the Magoosh math lesson videos, there’s a systematic way in which anyone can get the GCF. First we have to find the prime factorizations of both numbers.
54 = 6*9 = 2*3*3*3
81 = 9*9 = 3*3*3*3
What these prime factorizations have in common is three factors of three. Therefore,
GCF = 3*3*3 = 27
6) We will introduce variable that will cancel in the final ratio answer. Let’s call the radius of each small circle r.
That’s the area of the “holes.” Notice that the radius of the large circle is the radius of a small circle (r) plus the diameter of another small circle (2r). This means that the radius of the large circle is R = 3r. Therefore
The area of the shaded region is the area of the larger circle minus the area of the “holes.”
The fraction for which the question asks is the area of the shaded region divided by the area of the whole circle.
![]()

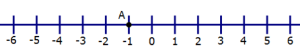
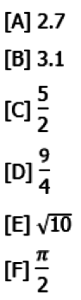





Leave a Reply