Here are six Praxis Math challenge problems. If you can handle these, you are in good shape for the Praxis Core Math Test!
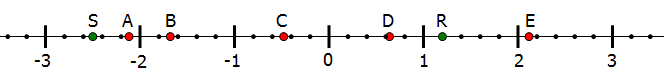
1) The number line shows seven points, each of them labeled with a letter of the alphabet. Consider the quotient
The coordinate of which of the following points is closest to this quotient?
(A) A
(B) B
(C) C
(D) D
(E) E
2) The Triangulum Galaxy is a distance from Earth of approximately D =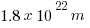 
. If light travels at a speed of c = 
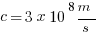and if 1 year =
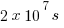, then approximately how many years does it take the light from the Triangulum Galaxy to reach Earth?
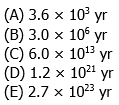
3) A certain municipal pump was able to pump five and five sixths cubic meters of water in one and three quarters of an hour. What is the hourly rate of this pump, in cubic meters per hour?
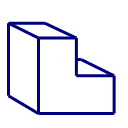
4) An L-shape is constructed by attaching three identical cubes, each with an edge length of 1 unit. The three cubes are permanently attached so that no seam is visible. When the exterior of this shape was painted, it took 28 ounces of paint. This first shape is just a scaled model. The final shape will be created in the same manner by joining three cubes with edge length 5. How many ounces of paint will be required to paint the exterior of this final shape?
(A) 140
(B) 280
(C) 700
(D) 1050
(E) 3500
5) Set J is a set of 150 numbers. The average of Set J is 62 and the range is 250. Set Q is a new set: each element in Set Q equals twice the corresponding number in Set J. What can we say about the average and range of Set Q?
(A) average of Set Q = 62; range of Set Q = 250
(B) average of Set Q > 62; range of Set Q = 250
(C) average of Set Q = 62; range of Set Q > 250
(D) average of Set Q > 62; range of Set Q < 250
(E) average of Set Q > 62; range of Set Q > 250
6) For a single evening’s performance, a certain theater company sold N orchestra tickets and M balcony tickets. A single orchestra ticket costs A dollars, and a single balcony ticket costs B dollars. These ticket sales were the company’s only source of revenue. The company had to pay a fee of R dollars to rent the space. In addition, there were T actors, and each actor had to be paid the same pay. Suppose after paying the rent and the actors’ pay, there was D dollars leftover from the ticket sales. Which of the following would represent the pay of a single actor?
Praxis Core Math
If you are a math pro, someone who studied something quantitative in college, then you should find the Praxis Core Mathematics Test quite manageable. You won’t find much on the Praxis that is more challenging than these problems.
What if math is not your very favorite thing in the world? What if you found these problems no fun at all? Suppose you bid a less-than-fond farewell to math sometime in high school, hoping that this ogre would never arise again, but now, because you want to be a teacher, you have to face the Praxis Core Mathematics Test and you have no confidence in your ability to do math: what should you do then? Well, in that case, I would passionately recommend the Magoosh Praxis product, because we have a full library of math lessons: even if you are starting from Square One, we can teach you everything you need and make you feel comfortable with math again. So, math-phobes who want to be teachers, take heart! Magoosh has your back!
Practice problem explanations
1) The coordinate of R appears to be about +1.2, and the coordinate of S appears to be about –2.5, so the desired quotient = (1.2)/(–2.5). We do not need to reach for a calculator or do a detailed calculation. First of all, we know positive divided by negative is negative, so the quotient will be negative. We also notice that the absolute value of the numerator is smaller than the absolute value of the denominator, so the quotient will have an absolute value of less than one. Thus, we need a quotient between –1 and 0. The only possible value is (C).
2) Since D = RT, it’s true that T = D/R. We will begin by dividing the distance by the rate to give us a time.
That’s the time in seconds. We need to multiply that by a conversion factor to change to years.
3) To get the rate, we need to dive the cubic meters of water divided by the number of hours. Both of these are given as mixed numerals. For the purposes of calculations such as division, mixed numerals are worse than useless. We have to convert the given mixed numerals to improper fractions, do the calculation with fractions, and change back to mixed numerals to select the answer.
That’s the rate in cubic meters per hour. Answer = (D)
4) For this, we use scale factor. Each length has been increased by 5, so k = 5. The surface of any shape is two-dimensional, and its area increases proportional to the square of k. The area, and the amount of paint, should be 25 times more.
new amount of paint = 25*(28 oz) = 50 * 14 oz = 100 * 7 oz = 700 oz
Notice that we used the doubling & halving trick to complete the calculation.
Answer = (C)
5) When we multiply all the numbers by two, the average gets multiplied by two, so the average increases. Also, the spacing between the numbers increases, so the range would be doubled as well: it also increase.
Answer = (E)
6) Let X be each actor’s salaries: that’s the number we have to find. The ticket sales provide the money in.
Money in = AN + BM
The expenses are the rent and the money paid to the actors for their salaries.
Money out = R + TX
The first minus the second leaves D, the leftover amount.
(AN + BM) – (R + TX) = D
We have to solve this for X.
AN + BM – R – TX = D
AN + BM – R = D + TX
AN + BM – R – D = TX
(AN + BM – R – D)/T = X
Answer = (A)
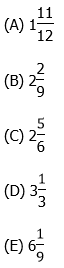
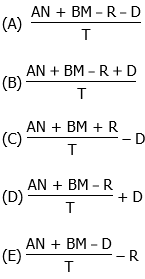
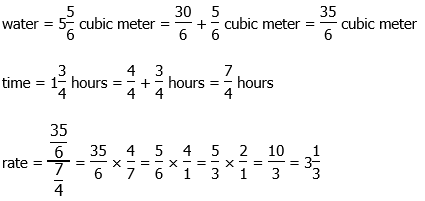
Leave a Reply